Question

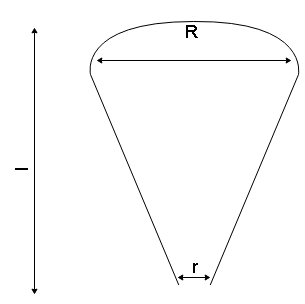
From a water reservoir, water is coming out through a vertical conical tube radius $ R $ and lower end of radius $ r $ . The length of the tube is $ l $ as shown in fig. Velocity of water coming through the upper end of the tube is?

Answer 1

Hint: Use the continuity equation to determine the ratio of velocities at the top and the bottom end then use Bernoulli's Equation to solve for the velocity of water coming out through the upper end.

Formula used:
-Continuity equation: $ {A_1}{v_1} = {A_2}{v_2} $ where $ A $ is the area of the tube at a particular point and $ v $ is the velocity of water at that point in the tube. Different positions in the tube are denoted by subscripts 1 and 2.
- Bernoulli’s equation: $ P + \rho gh + \dfrac{1}{2}\rho {v^2} = {\text{constant}} $ where $ P $ is the pressure, $ \rho $ is the density of the liquid, $ g $ is the gravitational acceleration, $ h $ is the height of the liquid above our reference point and $ v $ is the velocity of water

Complete step by step solution:
To solve this question, we start by using the continuity equation which relates the areas and velocities of the tube and the liquid in different parts of the tube. Writing the continuity equation for the upper and lower ends of the tube, we can write
 $ {A_{up}}{v_{up}} = {A_{low}}{v_{low}} $
Since the cross sections of the tube are circular, we can write
 $ \pi {R^2}{v_{up}} = \pi {r^2}{v_{low}} $
Hence the ratio of velocities in the upper end to the lower end can be written as:
 $ \dfrac{{{v_{up}}}}{{{v_{low}}}} = \dfrac{{{r^2}}}{{{R^2}}} $
Now Bernoulli’s equation tells us that
 $ P + \rho gh + \dfrac{1}{2}\rho {v^2} = {\text{constant}} $
Now, both the upper and lower ends of the tube are in contact with the atmosphere so they’ll have the same pressure. Further assuming the lower end as our reference height, the upper end will lie at a height of $ l $ from the bottom of the tube. So we can write
 $ \dfrac{1}{2}\rho v_{low}^2 = \rho gl + \dfrac{1}{2}\rho v_{up}^2 $
Now since $ \dfrac{{{v_{up}}}}{{{v_{low}}}} = \dfrac{{{r^2}}}{{{R^2}}} \Rightarrow {v_{low}} = {v_{up}}\dfrac{{{R^2}}}{{{r^2}}} $ , we can write
 $ \dfrac{1}{2}\rho v_{up}^2\dfrac{{{R^2}}}{{{r^2}}} = \rho gl + \dfrac{1}{2}\rho v_{up}^2 $
Taking the terms containing $ {v_{up}} $ on both sides, we can write:
 $ \dfrac{1}{2}\rho v_{up}^2\left( {\dfrac{{{R^2}}}{{{r^2}}} - 1} \right) = \rho gl $
Dividing both sides by $ \rho /2 $ we get
 $ v_{up}^2\left( {\dfrac{{{R^2}}}{{{r^2}}} - 1} \right) = 2gl $
 $ v_{up}^2 = \dfrac{{2gl}}{{\left( {\dfrac{{{R^2}}}{{{r^2}}} - 1} \right)}} $
Taking the square root on both sides, we get
 $ {v_{up}} = \sqrt {\dfrac{{2gl}}{{\left( {\dfrac{{{R^2}}}{{{r^2}}} - 1} \right)}}} $ .

Note:
The questions of fluid flow problems are usually solved by simultaneously using the continuity equation and Bernoulli’s equation. We only have to apply these equations at the upper end and the lower end of the tube and not at every point inside the tube