Question

From a solid cylinder of height 20 cm and diameter 12 cm, a conical cavity of height 8 cm and radius 6 cm is hollowed out. Find the T.S.A. of the remaining solid.

Answer 1

Hint: Here, we need to find the T.S.A. of the remaining solid. First, we will draw the figure and observe the areas which make up the T.S.A. of the remaining solid. We need to calculate the curved surface area of the cylinder, the area of the circular top of the cylinder, and the curved surface area of the cone using the respective formulae. Finally, we will add the three calculated areas together to get the T.S.A. of the remaining solid.

Formula Used: The radius of the base of the cone is half of its diameter, that is \[r = \dfrac{d}{2}\].
The area of the circular top or base of a cylinder or cone is given by the formula \[\pi {r^2}\], where \[r\] is the radius of the base/top of the cylinder or cone.
The curved surface area of a cylinder is given by the formula \[2\pi rh\], where \[r\] is the radius of the base of the cylinder, and \[h\] is the height of the cylinder.
The slant height \[l\] of a cone is given by the formula \[l = \sqrt {{r^2} + {h^2}} \], where \[r\] is the radius of the base of the cone, and \[h\] is the height of the cone.
The curved surface area of a cone is given by the formula \[\pi rl\], where \[r\] is the radius of the base of the cone, and \[l\] is the slant height of the cone.

Complete step-by-step answer:
The radius of the circular base of the cylinder is half of its diameter, that is \[r = \dfrac{d}{2}\].
Substituting \[d = 12\]cm in the formula, we get
Radius of the circular base of the cylinder \[ = \dfrac{{12}}{2} = 6\] cm
We can observe that the radius of the base of the cone and cylinder are equal.
Now, we will draw the diagram from the given information.
     

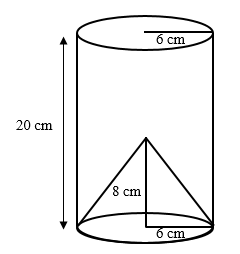
From the figure, we can observe that the T.S.A. of the remaining solid is the sum of the curved surface area of the cylinder, the curved surface area of the cone, and the area of the circular top of the cylinder.
First, we will find the area of the circular top of the cylinder.
The area of the circular top or base of a cylinder or cone is given by the formula \[\pi {r^2}\], where \[r\] is the radius of the base/top of the cylinder or cone.
Substituting \[r = 6\]cm in the formula, we get
\[ \Rightarrow \]Area of the circular top of the cylinder \[ = \pi {\left( 6 \right)^2}{\text{c}}{{\text{m}}^2}\]
Simplifying the expression, we get
\[ \Rightarrow \]Area of the circular top of the cylinder \[ = \pi \times 36 = 36\pi {\text{ c}}{{\text{m}}^2}\]
Now, we will find the curved surface area of the cylinder.
The curved surface area of a cylinder is given by the formula \[2\pi rh\], where \[r\] is the radius of the base of the cylinder, and \[h\] is the height of the cylinder.
Substituting \[r = 6\]cm and \[h = 20\]cm in the formula, we get
\[ \Rightarrow \]Curved surface area of the cylinder \[ = 2\pi \left( 6 \right)\left( {20} \right){\text{c}}{{\text{m}}^2}\]
Simplifying the expression, we get
\[ \Rightarrow \]Curved surface area of the cylinder \[ = 2\pi \times 120 = 240\pi {\text{ c}}{{\text{m}}^2}\]
Next, we will find the slant height and curved surface area of the cone.
The slant height \[l\] of a cone is given by the formula \[l = \sqrt {{r^2} + {h^2}} \], where \[r\] is the radius of the base of the cone, and \[h\] is the height of the cone.
Substituting \[r = 6\]cm and \[h = 8\]cm in the formula, we get
\[ \Rightarrow l = \sqrt {{6^2} + {8^2}} \]
Simplifying the expression, we get
\[ \Rightarrow l = \sqrt {36 + 64} \\
   \Rightarrow l = \sqrt {100} \\
  \therefore l = 10{\text{ cm}} \\
\]
Thus, the slant height of the cone is 10 cm.
The curved surface area of a cone is given by the formula \[\pi rl\], where \[r\] is the radius of the base of the cone, and \[l\] is the slant height of the cone.
Substituting \[r = 6\]cm and \[l = 10\]cm in the formula, we get
\[ \Rightarrow \]Curved surface area of the cone \[ = \pi \left( 6 \right)\left( {10} \right){\text{c}}{{\text{m}}^2}\]
Simplifying the expression, we get
\[ \Rightarrow \]Curved surface area of the cone \[ = \pi \times 60 = 60\pi {\text{ c}}{{\text{m}}^2}\]
Now, the T.S.A. of the remaining solid is the sum of the curved surface area of the cylinder, the curved surface area of the cone, and the area of the circular top of the cylinder.
Therefore, we get
\[ \Rightarrow \] T.S.A. of the remaining solid \[ = 240\pi + 60\pi + 36\pi = 336\pi {\text{ c}}{{\text{m}}^2}\]
Substituting \[\pi = \dfrac{{22}}{7}\] in the expression, we get
\[ \Rightarrow \]T.S.A. of the remaining solid \[ = \left( {336 \times \dfrac{{22}}{7}} \right){\text{ c}}{{\text{m}}^2}\]
Simplifying the expression, we get
\[\therefore \] T.S.A. of the remaining solid \[ = \left( {48 \times 22} \right){\text{ c}}{{\text{m}}^2} = 1056{\text{ c}}{{\text{m}}^2}\]
Therefore, we get the T.S.A. of the remaining solid as 1056 \[{\text{c}}{{\text{m}}^2}\].

Note: A common mistake is to add the total surface area of the cone and the total surface area of the cylinder to find the total surface area of the remaining solid. This is incorrect. We need to carefully observe the figure to determine the areas of which parts make up the total surface area of the remaining solid.