Question

From a point P outside line segment AB=6cm, construct a line PQ parallel to \[AB\].

Answer 1

Hint: To draw a parallel from a line segment to a point outside the line segment, firstly draw a line segment AB=6cm, then mark a point P outside of the line segment. Join the point P to the line segment. Measure the angle which the line from the point P makes with the line segment \[AB\] by making an arc and retrace the angle at the point P. Now, measure the length of the arc that intersects the line from the point P and the line segment \[AB\] and make a second arc on the retraced angle at the point P. Join the point P with the intersection of the arcs. We get a line parallel to the line segment \[AB\].

Complete step-by-step solution:
Parallel lines are a set of lines which never intersect no matter how far the lines are stretched. These can be compared to the train tracks that always run parallel to each other but never intersect. These lines have certain properties which will help us in the construction of these parallel lines. We will see those properties as we proceed.
According to the question, we have to construct a parallel line from a line with a given length (line segment) to a point which is outside of that line segment. We will do step wise construction:
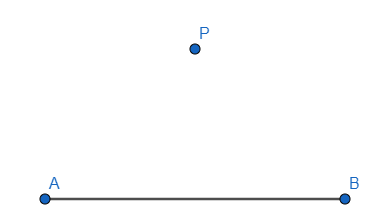
Step 1: Draw a line AB=6cm and label it as well.

Step 2: Now, mark a point P, anywhere outside the line segment \[AB\]
     

Step 3: Join the point P to a point (let’s say C) on the line segment \[AB\], we have

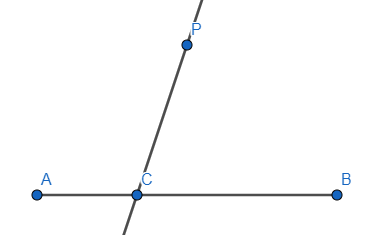
We know that parallel lines have congruent corresponding angles, we will use this property of the parallel lines to construct the parallel lines.
Step 4: Taking point C as the centre makes an arc intersecting the line \[PC\] and the line segment \[AB\].

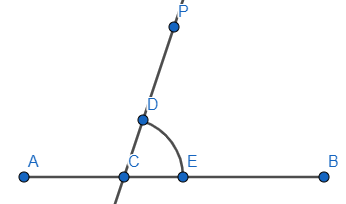
Step 5: Similarly, draw an arc taking P as the centre, we have,

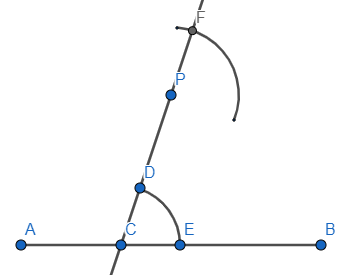
Step 6: Now the length of the arc intersecting the line segment \[AB\] and the line \[PC\], that measure the arc \[DE\] and make a second arc taking the point F as the centre, and then join the intersection of the arcs with the point P. We get

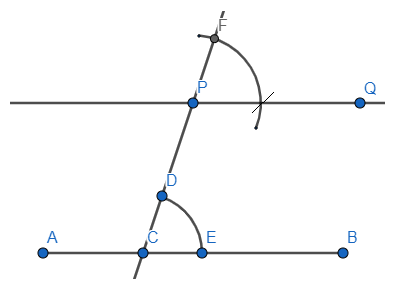
Therefore, we obtain \[PQ\] parallel to the line segment \[AB\].
To check whether the lines we obtained are parallel or not, we will use the property that in parallel lines the corresponding angles are equal. That is, we have to check if
$\angle DCB = \angle FPQ$
 or not. Measuring these angles, we get the values of these angles as:
$\angle DCB =71.5{6}^{\circ}$
$\angle FPQ =71.5{6}^{\circ}$
So, we see that both these angles are equal, therefore, we obtained parallel lines.

Note: Measuring of the arcs should be done neatly, as the entire construction of the parallel lines is depended on this step. After the construction of the parallel lines, never assume that they are definitely parallel, always check if the corresponding angles are congruent (or same) or not, only then your question is completed.