Question

From a point 20 m away from the foot of the tower, the angle of elevation of the top of the tower is ${30^ \circ }$ . Find the height of the tower.
A) 10 m
B) 11.56 m
C) 20.21 m
D) None of these

Answer 1

Hint: We will first form a triangle to represent the same situation graphically and thus use the trigonometric values to find the required length of the tower using the distance and the angle given to us and thus we have the answer.

Complete step-by-step solution:
Let us represent the same situation using a figure as given below where AB represents the tower and C is the point from which the tower is being observed with some angle of elevation.

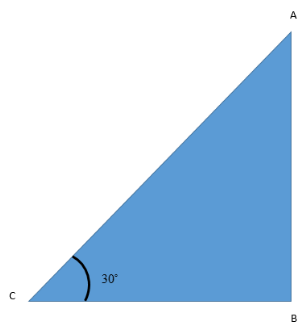
Here, in this picture, AB is the tower whose height we are required to find. Let C be the point from which the angle of elevation is taken. BC is the distance which is given to be 20 m in the question.
Since, we know that $\tan \theta = \dfrac{{Perpendicular}}{{Base}}$.
Replacing $\theta $ by C in the above formula, we will get:-
$ \Rightarrow \tan C = \dfrac{{AB}}{{BC}}$
Now, putting in the given data in the question, we will then obtain:-
$ \Rightarrow \tan \left( {{{30}^ \circ }} \right) = \dfrac{{AB}}{{20}}$
Since, we know that $\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}$, putting this in above expression, we will then obtain:-
$ \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{AB}}{{20}}$
Rearranging the terms in above expression to get:-
$ \Rightarrow AB = \dfrac{{20}}{{\sqrt 3 }}m$
Solving the RHS, we will get: AB = 11.56 m

$\therefore $ The correct option is (B) 11.56 m.

Note: The students must note that in case they forget the value of $\tan \theta $ or $\tan {30^ \circ }$, they may use the fact that:-
$\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }}$ And thus use the cosine and sine values for the same and we will get the required answer.
The students must note that $\dfrac{{20}}{{\sqrt 3 }}$ can be written as $\dfrac{{20}}{{\sqrt 3 }} \times \dfrac{{\sqrt 3 }}{{\sqrt 3 }} = \dfrac{{20\sqrt 3 }}{3}$
Since, we can now calculate 20 divided by 2 which is equal to $\dfrac{{20}}{3} = 6.666...$ and now if we multiply it by $\sqrt 3 $, we will then get the required answer which is 11.56 m
The students must note that this is the application of trigonometric values. Trigonometry is used in various fields like engineers use it to make sure that the structures are fine and so many more as well.