Question

Four point charges ${{q}_{A}}=2\mu C,$ ${{q}_{B}}=-5\mu C,$ ${{q}_{C}}=2\mu C,$ ${{q}_{D}}=-5\mu C,$ are located at the corners of a square ABCD of side 10cm. What is the force on charge of $1\mu C,$ placed at the center of the square?

Answer 1

Hint: State the Coulomb’s law and hence write the expression for the force of attraction or repulsion between two charges. Find the magnitude and direction of each force acting on charge Q due to charges at the corners of the square ABCD. Add or compare the forces acting on Q. Conclude resultant of forces of equal magnitude and acting in opposite directions is zero.

Complete answer:

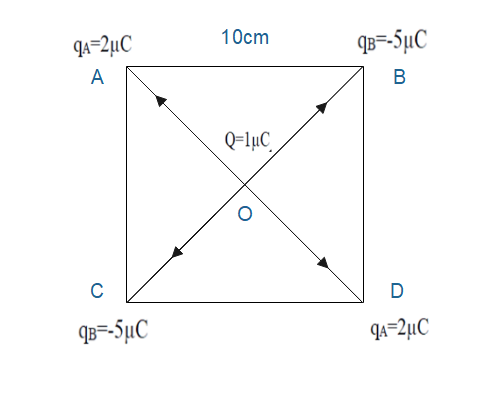
Let assume point charges ${{q}_{A}}=2\mu C,$${{q}_{B}}=-5\mu C,$${{q}_{C}}=2\mu C,$${{q}_{D}}=-5\mu C,$be located at corners A, B, C, and D of square ABCD respectively. Let $\text{Q}=1\mu C,$be at center O of the square.
The force between two point charges ${{q}_{1}}$and ${{q}_{2}}$distance r apart is given by coulomb’s law which states that the force of attraction or repulsion between two point charges is directly proportional to the product of their charges and inversely proportional two the square of the distance between them. Thus,
$\begin{align}
  & F\propto \dfrac{{{q}_{1}}{{q}_{2}}}{{{r}^{2}}} \\
 & F=K\dfrac{{{q}_{1}}{{q}_{2}}}{{{r}^{2}}} \\
\end{align}$
Where K is the constant of proportionality.
In vector form, Coulomb’s law can be written as
$\vec{F}=K\dfrac{{{q}_{1}}{{q}_{2}}}{{{r}^{2}}}\hat{r}$
Thus, the force acting on charge Q due to charge ${{q}_{A}}$is
${{F}_{A}}=K\dfrac{Q{{q}_{A}}}{AO}$
Force acting on charge Q due to charge ${{q}_{B}}$is
${{F}_{B}}=K\dfrac{Q{{q}_{B}}}{BO}$
Force acting on charge Q due to charge ${{q}_{C}}$is
${{F}_{C}}=K\dfrac{Q{{q}_{C}}}{CO}$
Force acting on charge Q due to charge ${{q}_{D}}$is
${{F}_{D}}=K\dfrac{Q{{q}_{D}}}{DO}$
We have, ${{q}_{A}}={{q}_{C}}$and AO=CO,
${{F}_{A}}={{F}_{C}}$(in magnitude)
But forces ${{F}_{A}}$and ${{F}_{C}}$ are directed towards O,
${{\overset{\scriptscriptstyle\rightharpoonup}{F}}_{A}}=-{{\overset{\scriptscriptstyle\rightharpoonup}{F}}_{C}}$
Thus, the force acting on charge Q due to charges ${{q}_{A}}$and ${{q}_{C}}$are equal in magnitude but opposite in direction. Therefore they cancel out each other.
Similarly, we have, ${{q}_{B}}={{q}_{D}}$and BO=DO,
${{F}_{B}}={{F}_{D}}$(in magnitude)
But forces ${{F}_{B}}$and ${{F}_{D}}$are directed towards O,
${{\overset{\scriptscriptstyle\rightharpoonup}{F}}_{B}}=-{{\overset{\scriptscriptstyle\rightharpoonup}{F}}_{D}}$
Thus, force acting on charge Q due to charges ${{q}_{B}}$and ${{q}_{D}}$are equal in magnitude but opposite in direction. Therefore they cancel out each other.
Hence, the total force acting on charge Q due to charges at the corners of square ABCD is zero.

Note:
Carefully write Coulomb’s law in magnitude and vector form. Since force is a vector, you have to consider both the magnitude as well as the direction. The forces acting in opposite directions but having equal magnitude contribute to zero. Coulomb’s law is valid for only point charges. If you have a system of two or more point charges then use the principle of superposition to calculate resultant force.