Question

Four charges $ + q $ , $ + q $ , $ - q $ and $ - q $ are replaced at corners A,B,C, and D of a square of side ‘a’, arranged in the given order. Calculate the intensity of the Electric Field at the center of the square where $ Q $ is placed.
(A) $ zero $
(B) $ \dfrac{{K4\sqrt 2 qQ}}{{{a^2}}} $
(C) $ \dfrac{{K4qQ}}{{{a^2}}} $
(D) $ \dfrac{{K2\sqrt 2 qQ}}{{{a^2}}} $

Answer 1

Hint To solve this question, we have to calculate the electric field due to each charge placed at the corner. Then we need to perform the vector summation of these fields to get the net electric field at the center.

Formula Used: The formula used in this solution is given as,
 $ \Rightarrow E = \dfrac{{Kq}}{{{r^2}}} $
Here, $ E $ is the electric field, $ q $ is the charge, $ r $ is the distance between the charge $ q $ and the test charge $ Q $ , and $ K = \dfrac{1}{{4\pi {\varepsilon _\circ }}} $ where, $ {\varepsilon _\circ } $ is the permittivity in free space,
 $ \Rightarrow F = QE $
Here, $ F $ is the electric force due to an electric field $ E $ on a test charge $ Q $ .

Complete step by step answer
Let us first try to represent the data given in the question diagrammatically.

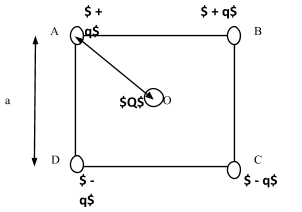
Now, if we let a point P at the midpoint of AD, then, using Pythagoras theorem we can write,
 $\Rightarrow A{O^2} = A{P^2} + P{O^2} $

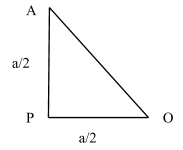
This gives us,
 $ \Rightarrow AO = \sqrt {{{\left( {\dfrac{a}{2}} \right)}^2} + {{\left( {\dfrac{a}{2}} \right)}^2}} $
 $ \Rightarrow AO = \dfrac{a}{{\sqrt 2 }} $
Now using the fact that opposite charges attract each other and the same charges repel each other, Let us show diagrammatically, how the following Electric Fields from the 4 charges will act at the center O.

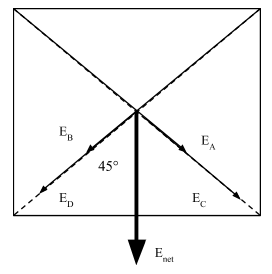
In the figure we get the angle to be 45°, because we know that each side makes an angle of 90° with the other side and the diagonal bisects the angle into two equal parts. Hence, by the property of alternate angles, we get,
 $ \Rightarrow \angle ACO = \angle CO{E_{net}} = 45^\circ $
We already know that since Electric Fields follow the principle of superposition, we can write,
 $ \Rightarrow \overrightarrow {{E_{net}}} = \overrightarrow {{E_A}} + \overrightarrow {{E_B}} + \overrightarrow {{E_C}} + \overrightarrow {{E_D}} $
Now, using the diagram drawn above, we get, $ {E_{net}} $ as,
 $\Rightarrow \overrightarrow {{E_{net}}} = \left| {\overrightarrow {{E_A}} } \right|\cos 45 + \left| {\overrightarrow {{E_B}} } \right|\cos 45 + \left| {\overrightarrow {{E_C}} } \right|\cos 45 + \left| {\overrightarrow {{E_D}} } \right|\cos 45 $
Now, if we let $ E $ to be the magnitude of Electric field due to a single charge, i.e.
 $\Rightarrow E = \left| {\overrightarrow {{E_A}} } \right| $
 $\Rightarrow E = \dfrac{{Kq}}{{{{\left( {\dfrac{a}{{\sqrt 2 }}} \right)}^2}}} $
We can easily infer that,
 $\Rightarrow E = \left| {\overrightarrow {{E_A}} } \right| = \left| {\overrightarrow {{E_B}} } \right| = \left| {\overrightarrow {{E_C}} } \right| = \left| {\overrightarrow {{E_D}} } \right| $
So, we can write the net Electric Field as,
 $\Rightarrow \overrightarrow {{E_{net}}} = E\cos 45 + E\cos 45 + E\cos 45 + E\cos 45 $
 $ \Rightarrow \overrightarrow {{E_{net}}} = 4E\cos 45 $
Now since we know the value of E and $ \cos 45 = \dfrac{1}{{\sqrt 2 }} $
Thus, we get the net Electric field as,
$ \overrightarrow {{E_{net}}} = 4\left( {\dfrac{{Kq}}{{\dfrac{{{a^2}}}{2}}}} \right)\left( {\dfrac{1}{{\sqrt 2 }}} \right) $
$ \Rightarrow \overrightarrow {{E_{net}}} = 4\left( {\dfrac{{2Kq}}{{{a^2}}}} \right)\left( {\dfrac{1}{{\sqrt 2 }}} \right) $
This gives us,
 $ \Rightarrow \overrightarrow {{E_{net}}} = \dfrac{{4\sqrt 2 Kq}}{{{a^2}}} $
So, we get the intensity of the electric field as,
 $ \Rightarrow F = QE $
 $ \Rightarrow F = \dfrac{{4\sqrt 2 KqQ}}{{{a^2}}} $
$ \therefore $ Option (B) is the correct option.

Note
We should not forget that the electric field is a vector quantity, not a scalar quantity. So, the net electric field at the centre of the square cannot be obtained by the direct summation. The electric field vectors first need to be resolved into perpendicular components, and then the algebraic addition must be performed.