Question

Form the differential equation of the family of circles in the first quadrant, which touches the coordinate axes.

Answer 1

Hint:Assume that the radius of the circle is r unit. The equation of circle in first quadrant which touches the coordinate axes and having radius r is ${{\left( x-r \right)}^{2}}+{{\left( y-r \right)}^{2}}={{r}^{2}}$. Now differentiate the equation with respect to x. From that expression find out the value of r and put it back in the equation of the circle to get the required equation.

Complete step by step answer:
Let the radius of the circle is r unit.
It is given that the circle touches both the coordinate axes in the first quadrant. That means the circle touches the x axis as well as the y axis. Therefore the center of the circle will be at $\left( r,r \right)$.

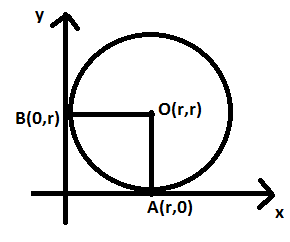
The equation of a circle in the first quadrant which touches the coordinate axes with center at $\left( r,r \right)$ and having radius r is:
${{\left( x-r \right)}^{2}}+{{\left( y-r \right)}^{2}}={{r}^{2}}......(1)$
Now we will differentiate the equation (1) with respect to x.
$\Rightarrow \dfrac{d}{dx}\left[ {{\left( x-r \right)}^{2}}+{{\left( y-r \right)}^{2}} \right]=\dfrac{d}{dx}\left( {{r}^{2}} \right)$
$\Rightarrow \dfrac{d}{dx}{{\left( x-r \right)}^{2}}+\dfrac{d}{dx}{{\left( y-a \right)}^{2}}=\dfrac{d}{dx}\left( {{r}^{2}} \right)......(2)$
We know that the radius r is a constant quantity. If we differentiate a constant quantity with respect to x, it will become zero. Therefore our right hand side of the equation will become zero.
In the left hand side we will apply the following rule of differentiation,
$\dfrac{d}{dx}{{\left( f\left( x \right) \right)}^{r}}=r{{\left( f\left( x \right) \right)}^{r-1}}\dfrac{d}{dx}f\left( x \right)$
Therefore from equation (2) we will get,
$\Rightarrow 2{{\left( x-r \right)}^{2-1}}\dfrac{d}{dx}\left( x-r \right)+\dfrac{d}{dy}{{\left( y-r \right)}^{2}}\times \dfrac{dy}{dx}=0$
$\Rightarrow 2\left( x-r \right)\times \left( \dfrac{d}{dx}\left( x \right)-\dfrac{d}{dx}\left( r \right) \right)+2\left( y-r \right)\times \left( \dfrac{d}{dy}\left( y \right)-\dfrac{d}{dy}\left( r \right) \right)\times \dfrac{dy}{dx}=0$
Here r is constant. Therefore differentiation of r with respect to any other variable will be zero.
$\Rightarrow 2\left( x-r \right)\times \left( 1-0 \right)+2\left( y-r \right)\times \left( 1-0 \right)\times \dfrac{dy}{dx}=0$
$\Rightarrow 2\left[ \left( x-r \right)+\left( y-r \right)\dfrac{dy}{dx} \right]=0$
$\Rightarrow x-r+\left( y-r \right)\dfrac{dy}{dx}=0$
Now we will find out the value of r from the above equation.
$\Rightarrow x+y\dfrac{dy}{dx}-r-r\dfrac{dy}{dx}=0$
$\Rightarrow -r\left( 1+\dfrac{dy}{dx} \right)=-\left( x+y\dfrac{dy}{dx} \right)$
We can cancel out the negative sign from both sides of the equation. Therefore,
$\Rightarrow r\left( 1+\dfrac{dy}{dx} \right)=x+y\dfrac{dy}{dx}$
Now divide both sides of the equation by $\left( 1+\dfrac{dy}{dx} \right)$.
$\Rightarrow r=\dfrac{x+y\dfrac{dy}{dx}}{1+\dfrac{dy}{dx}}$
Now we will put the value of r in equation (1).
Therefore,
${{\left( x-\dfrac{x+y\dfrac{dy}{dx}}{1+\dfrac{dy}{dx}} \right)}^{2}}+{{\left( y-\dfrac{x+y\dfrac{dy}{dx}}{1+\dfrac{dy}{dx}} \right)}^{2}}={{\left( \dfrac{x+y\dfrac{dy}{dx}}{1+\dfrac{dy}{dx}} \right)}^{2}}$
Now we will simplify the above expression as much as we can.
$\Rightarrow {{\left( \dfrac{x+x\dfrac{dy}{dx}-x-y\dfrac{dy}{dx}}{1+\dfrac{dy}{dx}} \right)}^{2}}+{{\left( \dfrac{y+y\dfrac{dy}{dx}-x-y\dfrac{dy}{dx}}{1+\dfrac{dy}{dx}} \right)}^{2}}=\dfrac{{{\left( x+y\dfrac{dy}{dx} \right)}^{2}}}{{{\left( 1+\dfrac{dy}{dx} \right)}^{2}}}$
Here we can cancel out a few opposite terms.
$\Rightarrow \dfrac{{{\left( x\dfrac{dy}{dx}-y\dfrac{dy}{dx} \right)}^{2}}}{{{\left( 1+\dfrac{dy}{dx} \right)}^{2}}}+\dfrac{{{\left( y-x \right)}^{2}}}{{{\left( 1+\dfrac{dy}{dx} \right)}^{2}}}=\dfrac{{{\left( x+y\dfrac{dy}{dx} \right)}^{2}}}{{{\left( 1+\dfrac{dy}{dx} \right)}^{2}}}$
In both sides of the equation the denominators are the same. Therefore we can cancel out the denominators from both sides of the equation.
$\Rightarrow {{\left( \dfrac{dy}{dx} \right)}^{2}}{{\left( x-y \right)}^{2}}+{{\left( y-x \right)}^{2}}={{\left( x+y\dfrac{dy}{dx} \right)}^{2}}$
$\Rightarrow {{\left( x-y \right)}^{2}}\left( {{\left( \dfrac{dy}{dx} \right)}^{2}}+1 \right)={{\left( x+y\dfrac{dy}{dx} \right)}^{2}}$
This is the required differential equation.
Therefore, the differential equation of the family of the circles in the first quadrant which touches the coordinate axes is:
$\Rightarrow {{\left( x-y \right)}^{2}}\left( {{\left( \dfrac{dy}{dx} \right)}^{2}}+1 \right)={{\left( x+y\dfrac{dy}{dx} \right)}^{2}}$

Note: We need to be careful when we are differentiating with respect to x. We can make mistakes while we are differentiating the term ${{\left( y-r \right)}^{2}}$ with respect to x. Here we need to change the derivative as follows:
$\dfrac{d}{dx}{{\left( y-r \right)}^{2}}=\dfrac{d}{dy}{{\left( y-r \right)}^{2}}\times \dfrac{dy}{dx}$