Question

Form the differential equation of all the circles which touch the x-axis at the origin?

Answer 1

Hint: We start solving the problem by assuming the equation of the circles and use the condition that the circle passes through the origin and touches the x-axis only at origin to get the resultant equation of the circle. We then start differentiating the obtained equation of circles on both sides with respect to x to get the value of arbitrary constants present in the equation. We then substitute this obtained value of the arbitrary constant in the equation of circles and make necessary calculations to get the required result.

Complete step-by-step solution
According to the problem, we need to find the differential equation of all the circles which touch the x-axis at the origin.
Let us first find the equation of the circle touching the x-axis at the origin.

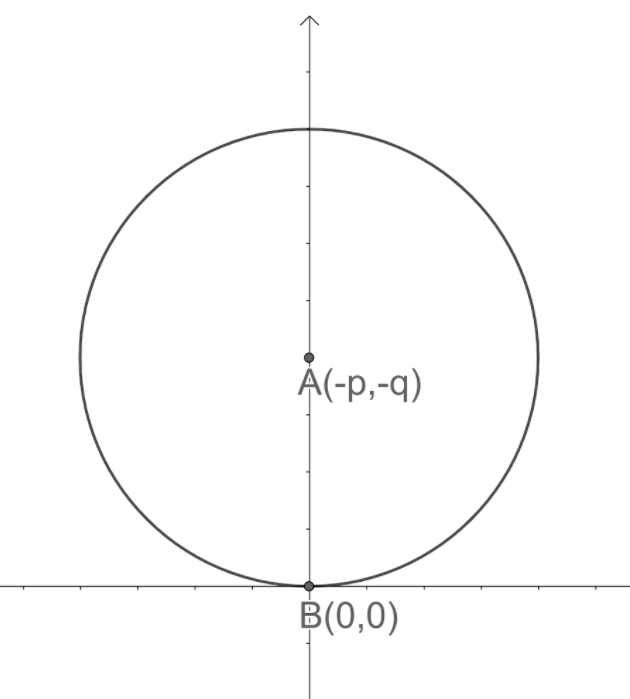
Let us assume the equation of the circle to be ${{x}^{2}}+{{y}^{2}}+2px+2qy+c=0$. According to the problem, we are given that this circle touches the x-axis at the origin. So, this gives us that the circle passes through the origin.
Let us substitute the point $B\left( 0,0 \right)$ in the circle ${{x}^{2}}+{{y}^{2}}+2px+2qy+c=0$.
So, we get ${{\left( 0 \right)}^{2}}+{{\left( 0 \right)}^{2}}+2p\left( 0 \right)+2q\left( 0 \right)+c=0$.
$\Rightarrow c=0$.
We get the equation of the circle as ${{x}^{2}}+{{y}^{2}}+2px+2qy=0$.
Now, let us substitute $y=0$ in the circle ${{x}^{2}}+{{y}^{2}}+2px+2qy=0$ as the circle touches x-axis.
So, we get ${{x}^{2}}+{{\left( 0 \right)}^{2}}+2px+2q\left( 0 \right)=0$.
$\Rightarrow {{x}^{2}}+{{\left( 0 \right)}^{2}}+2px+2q\left( 0 \right)=0$.
$\Rightarrow {{x}^{2}}+2px=0$.
$\Rightarrow x\left( x+2p \right)=0$.
$\Rightarrow x=0$ or $x=-2p$. But according to the problem, the circle ${{x}^{2}}+{{y}^{2}}+2px+2qy=0$ touches the x-axis at the only origin. This tells that the other value of x should also be 0.
So, we get $-2p=0\Leftrightarrow p=0$.
So, we get the equation of circles touching x-axis at origin as ${{x}^{2}}+{{y}^{2}}+2qy=0$ ---(1).
We need to find the differential equation for this family of circles.
Let us differentiate both sides of ${{x}^{2}}+{{y}^{2}}+2qy=0$ with respect to x.
So, we get $\dfrac{d}{dx}\left( {{x}^{2}}+{{y}^{2}}+2qy \right)=\dfrac{d}{dx}\left( 0 \right)$.
$\Rightarrow \dfrac{d}{dx}\left( {{x}^{2}} \right)+\dfrac{d}{dx}\left( {{y}^{2}} \right)+\dfrac{d}{dx}\left( 2qy \right)=0$.
$\Rightarrow 2x+2y\dfrac{dy}{dx}+2q\dfrac{dy}{dx}=0$.
$\Rightarrow q\dfrac{dy}{dx}=-x-y\dfrac{dy}{dx}$.
$\Rightarrow q=-\dfrac{x}{\dfrac{dy}{dx}}-y$ ---(2).
Let us substitute equation (2) in equation (1).
$\Rightarrow {{x}^{2}}+{{y}^{2}}+2\left( -\dfrac{x}{\dfrac{dy}{dx}}-y \right)y=0$.
$\Rightarrow {{x}^{2}}+{{y}^{2}}-\dfrac{2xy}{\dfrac{dy}{dx}}-2{{y}^{2}}=0$.
$\Rightarrow {{x}^{2}}-{{y}^{2}}-\dfrac{2xy}{\dfrac{dy}{dx}}=0$.
$\Rightarrow \dfrac{\left( {{x}^{2}}-{{y}^{2}} \right)\dfrac{dy}{dx}-2xy}{\dfrac{dy}{dx}}=0$.
$\Rightarrow \left( {{x}^{2}}-{{y}^{2}} \right)\dfrac{dy}{dx}-2xy=0$.
So, we have found the differential equation of all circles touching x-axis as $\left( {{x}^{2}}-{{y}^{2}} \right)\dfrac{dy}{dx}-2xy=0$.
$\therefore$ The differential equation of all circles touching x-axis as $\left( {{x}^{2}}-{{y}^{2}} \right)\dfrac{dy}{dx}-2xy=0$.

Note: We should know that the circles touching the x-axis at origin will have their centers on the y-axis. We should know that q is called an arbitrary constant as it represents equations of all the circles satisfying the given condition. If we have ‘n’ arbitrary constants in the equations, we differentiate the equation ‘n’ times to get the values of all arbitrary constants. Similarly, we can expect problems to find the differential equation of the circles which touch the y-axis at the origin.