Question

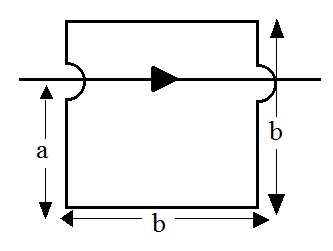
For the situation shown in the figure, Flux through the square loop is:

A. $\left( \dfrac{ \mu_0 i a }{2 \pi} \right) \ln \left( \dfrac{ a }{2a - b} \right) $
B. $\left( \dfrac{ \mu_0 i a }{2 \pi} \right) \ln \left( \dfrac{ a }{2b - a} \right) $
C. $\left( \dfrac{ \mu_0 i b }{2 \pi} \right) \ln \left( \dfrac{ a }{b - a} \right) $
D. $\left( \dfrac{ \mu_0 i a }{2 \pi} \right) \ln \left( \dfrac{ 2a }{b - a} \right) $

Answer 1

Hint: Mark the direction of the magnetic field first with the help of Right Hand Thumb Rule. The net flux through the square coil will be due to whatever magnetic field will not cancel as in coming out and going in the coil.
Formula used:
The magnetic field around a current carrying wire is given as:
$B = \dfrac{ \mu_0 i}{2 \pi r}$
where r is the distance from the wire.
Magnetic flux
$\phi = B.A$

Complete answer:
The resultant flux through the square loop will be a sum of magnetic field coming out and magnetic field going in. Above the wire, we can observe that the magnetic field appears to be coming out and below the wire the magnetic field appears to be going in. We are given that the square loop is placed unequally on the wire, this means the square loop has more area below the wire as compared to its area above the wire. Therefore it will be this extra area of the square loop below the wire that will give us a resultant flux (because the rest of it will cancel).

We already know that the magnetic field at a distance x from a current carrying conductor is given as:
$B = \dfrac{ \mu_0 i}{2 \pi x}.$
To find out the flux we need to integrate (surface integral) in the net area below the wire going from b-a to a. (As b-a distance above and below the wire have opposing flux so we just try to eliminate the integration in that part).
We consider a strip of area b.dx. The flux through this strip is

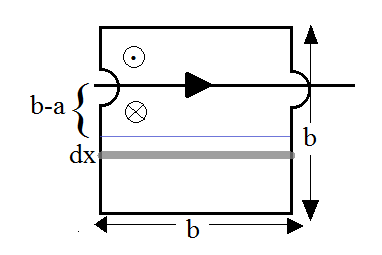
$d \phi = B b dx$
Or
$d \phi = \dfrac{ \mu_0 i}{2 \pi x} b dx$
Integrating both sides we get:
$\int d \phi = \int_{b-a}^{a} \dfrac{ \mu_0 i b}{2 \pi x} dx $
$\int d \phi = \dfrac{ \mu_0 i b}{2 \pi } \int_{b-a}^{a} \dfrac{dx}{x} $
$\phi = \dfrac{ \mu_0 i b}{2 \pi } \ln \left(\dfrac{a}{b-a} \right)$

So, the correct answer is “Option C”.

Note:
The semi circles in the diagram of the question suggest that the square loop is overlapping (without crossing) the infinite current carrying wire. Therefore it can be assumed to be present in the plane of the wire approximately. We can imagine the wire to be going along the x axis. So that the contribution of area (b-a) $\times$ b above and below this axis (wire) cancels.