Question

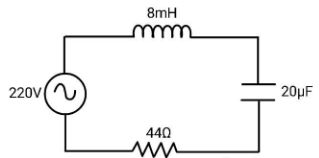
For the series LCR circuit shown in the figure, what is the resonance frequency and the amplitude of the current at the resonating frequency?

(A) $2500rad{s^{ - 1}}$ and $5\sqrt 2 A$
(B) $2500rad{s^{ - 1}}$ and $5A$
(C) $2500rad{s^{ - 1}}$ and $\dfrac{5}{{\sqrt 2 }}A$
(D) $25rad{s^{ - 1}}$ and $5\sqrt 2 A$

Answer 1

Hint: Here, an inductor, a capacitor and a resistor are connected in series and the combination is fed with an ac voltage of $220V$, which is basically an LCR circuit. Resonating frequency is the frequency at which the impedance of the circuit is minimum or in other words, the current is maximum. Find the current in the LCR circuit and derive the condition for maximum current. For finding current, use the vector method.

Complete step by step answer:
Vector method is a method to find the current in an ac circuit in which the resistances are considered as vectors. Let us consider the resistance of a resistor as a vector in the direction of positive x-axis of magnitude $R$, reactance of the capacitance as a vector pointing towards positive y-axis with magnitude ${X_C}$ and reactance of the inductor as a vector pointing towards negative y-axis with magnitude ${X_L}$.

The reactance of capacitor is ${X_C} = \dfrac{1}{{\omega C}}$ and that of inductor is ${X_L} = \omega L$, where $C$ is the capacitance of the capacitor, $L$ is the inductance of the inductor and $\omega $ is the angular frequency of the supply ac source. The impedance of the circuit will be given as $Z = \sqrt {{R^2} + {{\left( {{X_C} - {X_L}} \right)}^2}} $. The current in the LCR circuit will be \[I = \dfrac{V}{Z} = \dfrac{V}{{\sqrt {{R^2} + {{\left( {{X_C} - {X_L}} \right)}^2}} }}\]. In order to maximize the current \[ \to {X_C} - {X_L} = 0\].
\[
{X_C} = {X_L} \\
\Rightarrow \dfrac{1}{{\omega C}} = \omega L \\
\Rightarrow {\omega ^2} = \dfrac{1}{{LC}} \\\
\Rightarrow \omega = \dfrac{1}{{\sqrt {LC} }} \\
\]
This is the resonance frequency.

Let us substitute the values in order to get resonance frequency and the corresponding to it, the current in the circuit.
\[
\omega = \dfrac{1}{{\sqrt {LC} }} \\
\Rightarrow \omega = \dfrac{1}{{\sqrt {\left( {8 \times {{10}^{ - 3}}} \right)\left( {20 \times {{10}^{ - 6}}} \right)} }} \\
\Rightarrow \omega = 2500rad{s^{ - 1}} \\
\]
\[
I = \dfrac{V}{{\sqrt {{R^2} + {{\left( {{X_C} - {X_L}} \right)}^2}} }} \\
\Rightarrow I = \dfrac{{220}}{{\sqrt {{{\left( {44} \right)}^2} + {{\left( 0 \right)}^2}} }} \\
\therefore I = 5A \\ \]
Therefore, the resonance frequency and the amplitude of the current at the resonating frequency are $2500rad{s^{ - 1}}$ and $5A$.

Hence, option B is correct.

Note: In case of ac circuit, you should always use the vector method in order to find the current in the circuit. Keep in mind that depending on the reactance of the inductor and the capacitor, you can determine whether the current leads the emf or the other way round, that is the emf leading current. Also remember the value of reactance of both inductor and capacitor and also the value of the impedance of the circuit.