Question

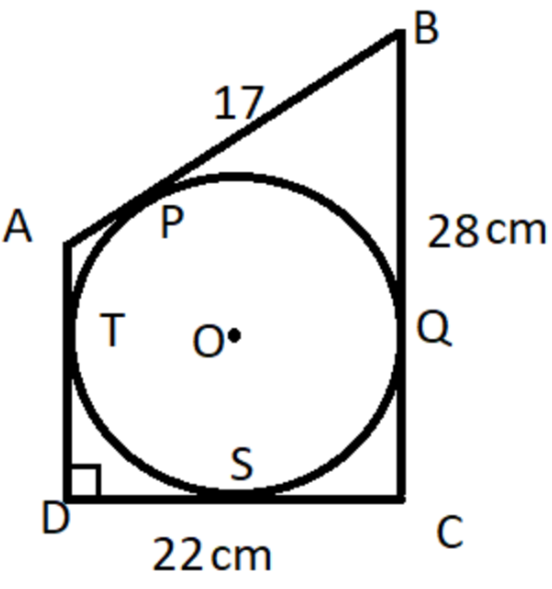
For the given figure, a circle is inscribed in a quadrilateral ABCD. If $BC=28cm$, $BP=17cm$, $CD=22cm$ and $AD\bot CD$. Find the radius of the circle.

Answer 1

Hint: We use the geometrical formula of tangents being of equal length from a fixed outside point. We draw a radius to compare it with the tangent whose length is a known element. Then comparing the length value, we get the radius length. We also need to use the interior angles formula for a quadrilateral to get the relation between the radius and the tangent.

Complete step-by-step solution:
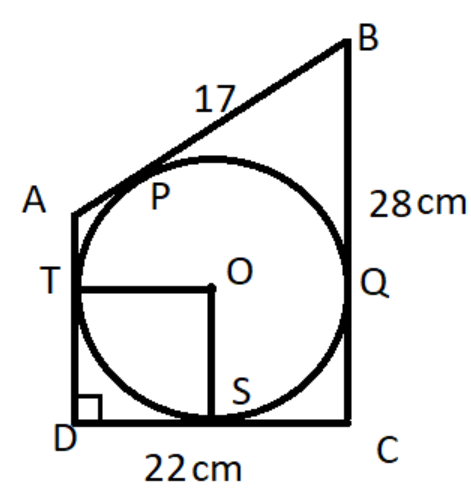
We are going to draw the two radii OT and OS from center O. Let radius be x cm.
Then, $OT=OS=xcm$.

We are going to use the geometrical formula of a tangent which tells us that lengths of tangents drawn from an external point to a circle are equal.
From an outside point, B two tangents have been drawn BP and BQ. The length of BP and BQ will be the same. So, $BP=BQ=17cm$.
Similarly, from outside point D, two tangents have been drawn DS and DT. The length of DS and DT will be the same.
And from point C two tangents have been drawn CS and CQ. The length of CS and CQ will be the same.
We found DS is a tangent of the circle at point S. OS is the radius.
So, $OS\bot DS$. It implies $\angle OSD={{90}^{\circ }}$.
It’s given that $AD\bot CD$ which means $\angle TDS={{90}^{\circ }}$.
In quadrilateral OTDS we add these two interior angles and get that \[\angle OSD+\angle TDS={{90}^{\circ }}+{{90}^{\circ }}={{180}^{\circ }}\] which tells us quadrilateral OTDS is a parallelogram.
[we know if the sum of two consecutive interior angles of a quadrilateral is it’s a parallelogram]
Now, $CQ=BC-BQ$.
We put the values to get the length of CQ.
The length of CQ is $CQ=BC-BQ=28-17=11cm$.
We know, $CS=CQ=11cm$.
It’s given $CD=22cm$.
So, the length of the DS will be $DS=CD-CS$.
We put the values to get the length of DS.
The length of DS is $DS=CD-CS=22-11=11cm$.
Now, OTDS is a parallelogram. So, the opposite sides are equal.
So, $DS=OT=OS=xcm$ as DS is equal to OT which is a radius.
Hence, $radius=OT=DS=11cm$.

Note: Although we drew two radii, we only used one of them to get to the solution. The radii mainly worked to form the quadrilateral. The reason of the quadrilateral being parallelogram can also be expressed through corresponding angles being similar of right angle.