Question

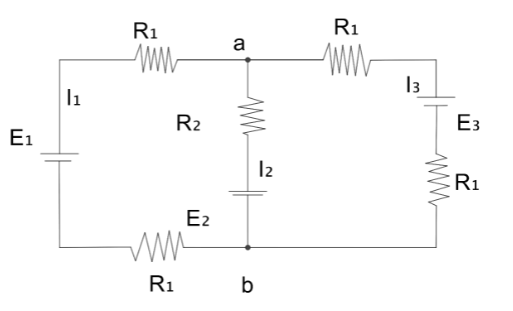
For the circuit shown, with ${R_1}{\text{ }} = {\text{ }}1{\text{ }}\Omega $, ${R_2}{\text{ }} = {\text{ }}2{\text{ }}\Omega $, ${E_1}{\text{ }} = {\text{ }}2{\text{ }}V$ and ${E_2}{\text{ }} = {\text{ }}{E_3}{\text{ }} = {\text{ }}4{\text{ }}V$, the potential difference between the points ‘$a$’ and ‘$b$’ is approximately (in $V$):

Answer 1

Hint:We will use the basic equations of equivalent resistance and potential difference. Finally, we will substitute the values in their respective positions and then calculate the actual numerical value.

Formulae Used:
${R_{Series}}{\text{ }} = {\text{ }}{R_1}{\text{ }} + {\text{ }}{R_2}{\text{ }} + {\text{ }}...{\text{ }} + {\text{ }}{R_n}$
$\Rightarrow \dfrac{1}{{{R_{Parallel}}}}{\text{ }} = {\text{ }}\dfrac{1}{{{R_1}}}{\text{ }} + {\text{ }}\dfrac{1}{{{R_2}}}{\text{ }} + {\text{ }}...{\text{ }} + {\text{ }}\dfrac{1}{{{R_n}}}$
And,
$\Rightarrow I{\text{ }} = {\text{ }}\dfrac{V}{R}$
$\Rightarrow V{\text{ }} = {\text{ }}IR$

Complete step by step answer:
Here, we have to calculate the potential difference between $a$ and $b$. Thus, we will calculate the resistances for each cell. For cell ${E_1}$, the net resistance will be
${R_1}{\text{ }} + {\text{ }}{R_1} = 2{R_1}$
Again, for the cell ${E_2}$, the resistance is ${R_2}$
Also, for the cell ${E_3}$, the resistance is
${R_1}{\text{ }} + {\text{ }}{R_1}{\text{ }} = {\text{ }}2{R_1}$
Now, the current out of cell ${E_1}$ will be $\dfrac{{{E_1}}}{{2{R_1}}}$.
Through ${E_2}$ is $\dfrac{{{E_2}}}{{{R_2}}}$
And, through ${E_3}$ is $\dfrac{{{E_3}}}{{2{R_1}}}$
Thus, total current through the circuit where $a$ and $b$ are the endpoints:
${I_{ab}}{\text{ }} = {\text{ }}\dfrac{{{E_1}}}{{2{R_1}}}{\text{ }} + {\text{ }}\dfrac{{{E_2}}}{{{R_2}}}{\text{ }} + {\text{ }}\dfrac{{{E_3}}}{{2{R_1}}}$

Now, if we consider the points $a$ and $b$ as the end points. All the individual cell circuits will be in parallel with each other. Thus, the net resistance will be
$\dfrac{1}{{{R_{ab}}}}{\text{ }} = {\text{ }}\dfrac{1}{{2{R_1}}}{\text{ }} + {\text{ }}\dfrac{1}{{{R_2}}}{\text{ }} + {\text{ }}\dfrac{1}{{2{R_1}}}$
Thus, the potential difference between $a$ and $b$ will be
${V_{ab}}{\text{ }} = {\text{ }}{I_{ab}}{\text{ }}{R_{ab}}$
This equation can also be written as
${V_{ab}}{\text{ }} = {\text{ }}\dfrac{{{I_{ab}}}}{{\dfrac{1}{{{R_{ab}}}}}}$
Now,
Substituting the values, we get
${V_{ab}}\, = {\text{ }}\dfrac{{\dfrac{{{E_1}}}{{2{R_1}}}{\text{ }} + {\text{ }}\dfrac{{{E_2}}}{{{R_2}}}{\text{ }} + {\text{ }}\dfrac{{{E_3}}}{{2{R_1}}}}}{{\dfrac{1}{{2{R_1}}}{\text{ }} + {\text{ }}\dfrac{1}{{{R_2}}}{\text{ }} + {\text{ }}\dfrac{1}{{2{R_1}}}}}$
Further, we get
${V_{ab}}{\text{ }} = {\text{ }}\dfrac{{2{E_1}{R_1}{R_2}{\text{ }} + {\text{ }}4{E_2}{R_1}^2{\text{ }} + {\text{ }}2{E_3}{R_1}{R_2}}}{{2{R_1}{R_2}{\text{ }} + {\text{ }}4{R_1}^2{\text{ }} + {\text{ }}2{R_1}{R_2}}}$

Taking $2{R_1}$ common from the numerator and the denominator and cancelling, we get
${V_{ab}}{\text{ }} = {\text{ }}\dfrac{{{E_1}{R_2}{\text{ }} + {\text{ }}2{E_2}{R_1}{\text{ }} + {\text{ }}{E_3}{R_2}}}{{2{R_2}\; + {\text{ }}2{R_1}}}$
Then, we get
${V_{ab}}{\text{ }} = {\text{ }}\dfrac{{({E_1}{\text{ }} + {\text{ }}{E_3}){R_2}{\text{ }} + {\text{ }}2{E_2}{R_1}}}{{2({R_1}{\text{ }} + {R_2})}}$
Now, substituting the given values in this equation, we get
${V_{ab}}{\text{ }} = {\text{ }}\dfrac{{(2{\text{ }} + {\text{ }}4){\text{ }} \times {\text{ }}2{\text{ }} + {\text{ }}2{\text{ }} \times {\text{ }}4{\text{ }} \times {\text{ }}1}}{{2{\text{ }} \times {\text{ }}(1{\text{ }} + {\text{ }}3)}}$
After further evaluation, we get
${V_{ab}}{\text{ }} = {\text{ }}\dfrac{{12{\text{ }} + {\text{ }}4}}{8}$
Then, we get
${V_{ab}}{\text{ }} = {\text{ }}\dfrac{{16}}{8}$
Thus, we get
$\therefore {V_{ab}}{\text{ }} = {\text{ }}2{\text{ }}V$

Hence, the potential difference between the points ‘$a$’ and ‘$b$’ is 2 V.

Note: Students often commit errors in considering the type of circuit it will form when we take some other point within the given circuit as end points. This would lead them applying the wrong formula and eventually reaching an incorrect answer. If students are confused with what the new circuit will be, it is always a safe method to redraw the circuit taking the new endpoints. This would reduce the possibility of committing a mistake.