Question

For the circuit shown in figure the rms current is

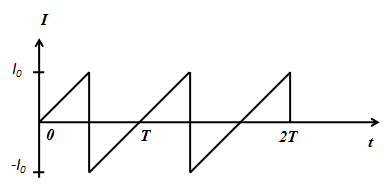
A. \[{I_0}\]
B. \[{I_0}/\sqrt 2 \]
C. \[{I_0}/\sqrt 3 \]
D. \[{I_0}/2\]

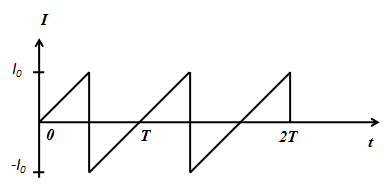
Answer 1

Hint: Identify the current I function in the region of \[0 < t < \dfrac{T}{2}\] and \[\dfrac{T}{2} < t < T\]. First, we will find the square of the current function and integrate over the region. After that, we can take the square root of obtained value and that will be rms value.

Complete step by step answer:
The rms is an abbreviation of root mean square value of a function. In order to do so, first we have to square the function then find its mean value and then at last square root of that value.
From the figure, we know the form of the current (\[I\]) function.
\[I = \dfrac{{2{I_0}}}{T}t\] for \[0 < t < \dfrac{T}{2}\]
And,
\[I = \dfrac{{2{I_0}}}{T}\left( {t - T} \right)\] for \[\dfrac{T}{2} < t < T\]

Since it is a period function in nature, we do not need to account the whole region. We will calculate the mean square speed in one time period T.

We take the square of the above equation as follows,
\[{I^2} = \dfrac{{4I_0^2}}{{{T^2}}}{t^2}\] for \[0 < t < \dfrac{T}{2}\]
And,
\[{I^2} = \dfrac{{4I_0^2}}{{{T^2}}}{\left( {t - T} \right)^2}\] for \[\dfrac{T}{2} < t < T\]

The mean of this function will be,
\[I_{mean}^2 = \int\limits_0^T {{I^2}} dt = \int\limits_0^{\dfrac{T}{2}} {{I^2}} dt + \int\limits_{\dfrac{T}{2}}^T {{I^2}} dt\]
\[ \Rightarrow I_{mean}^2 = \int\limits_0^{\dfrac{T}{2}} {\dfrac{{4I_0^2}}{{{T^2}}}{t^2}} dt + \int\limits_{\dfrac{T}{2}}^T {\dfrac{{4I_0^2}}{{{T^2}}}{{\left( {t - T} \right)}^2}} dt\]
\[ \Rightarrow I_{mean}^2 = \int\limits_0^{\dfrac{T}{2}} {\dfrac{{4I_0^2}}{{{T^2}}}{t^2}} dt + \int\limits_{\dfrac{T}{2}}^T {\dfrac{{4I_0^2}}{{{T^2}}}\left( {{t^2} - 2tT + {T^2}} \right)} dt\]
\[ \Rightarrow I_{mean}^2 = \dfrac{{4I_0^2}}{{{T^2}}}\left( {\left( {\dfrac{{{t^3}}}{3}} \right)_0^{\dfrac{T}{2}} + \left( {\dfrac{{{t^3}}}{3}} \right)_{\dfrac{T}{2}}^T - 2T\left( {\dfrac{{{t^2}}}{2}} \right)_{\dfrac{T}{2}}^T + {T^2}\left( t \right)_{\dfrac{T}{2}}^T} \right)\]
After simplifying the above equation further we get,
\[I_{mean}^2 = \dfrac{{4I_0^2}}{{{T^2}}}\left( {\dfrac{{{T^2}}}{{12}}} \right)\]
\[ \Rightarrow I_{mean}^2 = \dfrac{{I_0^2}}{3}\]
Now, root mean square of the current function will be,
\[{I_{rms}} = \sqrt {I_{mean}^2} = \sqrt {\dfrac{{I_0^2}}{3}} \]
\[ \Rightarrow {I_{rms}} = \dfrac{{{I_0}}}{{\sqrt 3 }}\]

So, the current answer is option (C).

Note:
 In case of an odd periodic function, the mean value of the function in one time period goes to zero. To understand the mean nature of the corresponding function, root mean square value is very important for odd periodic functions. By using the Fourier series identity we could have write the equation \[\int\limits_0^{\dfrac{T}{2}} {{I^2}} dt + \int\limits_{\dfrac{T}{2}}^T {{I^2}} dt = 2\int\limits_0^T {{I^2}} dt\] if the function is symmetric. But the function has different values in the respective regions, we cannot do so.