
For the circles ${x^2} + {y^2} - 10x + 16y + 89 - {r^2} = 0$and ${x^2} + {y^2} + 6x - 14y + 42 = 0$ which of the following is/are true.
(A) Number of integral values of r are 14 for which circles are intersecting.
(B) Number of integral values of r are 9 for which circles are intersecting.
(C) For r equal to 13, the number of common tangents is 3.
(D) For r equal to 21, the number of common tangents are 2.
Answer
576.3k+ views
Hint: The equations of two circles are given. Find their radii and their centres. Next, check if the sum of their radii is greater/equal/less than the distance between their centres. Note that, if two circles intersect, then the sum of their radii must be greater than the distance between their centres. By using these conditions we will get the required solution.
Complete step by step Answer:
We know that the general equation of a circle is given by $a{x^2} + b{y^2} + 2gx + 2fy + c = 0$ ,
∴ Its centre is located at\[ = ( - g,{\text{ }} - f)\]
And its radius is given by $ = \sqrt {{g^2} + {f^2} - c} {\text{ units}}$
Now, the equation of the first circle is given by ${x^2} + {y^2} - 10x + 16y + 89 - {r^2} = 0$
Therefore, its centre C1 is at \[(5, - 8)\]
And its radius r1 is given by
$ = \sqrt {{{(5)}^2} + {{\left( { - 8} \right)}^2} - \left( {89 - {r^2}} \right)} $
On simplification we get,
$ = \sqrt {25 + 64 - 89 + {r^2}} $
On adding first two terms and on simplification we get,
$ = r$units
Again, the equation of the second circle is given by ${x^2} + {y^2} + 6x - 14y + 42 = 0$
Therefore, its centre C2 is at \[( - 3,{\text{ }}7)\]
And its radius r2 is given by
$ = \sqrt {{{\left( { - 3} \right)}^2} + {{\left( 7 \right)}^2} - 42} $
On simplification we get,
$ = \sqrt {9 + 49 - 42} $
On adding the terms we get,
$ = \sqrt {16} $
On taking positive square root we get,
\[ = 4\] units
Now we know that the distance between the points (x1, y1) and (x2, y2) is given by
\[{\text{ }} = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \]
Therefore the distance between the centres of the two circles is
\[{C_1}{C_2} = \sqrt {{{\left( {5 + 3} \right)}^2} + {{\left( { - 8 - 7} \right)}^2}} \]
On simplification we get,
\[ = \sqrt {64 + 225} \]
On adding we get,
\[ = \sqrt {289} \]
On taking positive square root we get,
\[ = 17{\text{ }}\]units
Now, if these two circles intersect, therefore the sum of their radii must be greater than the distance between their centres. In that case the number of common tangents will be 2.
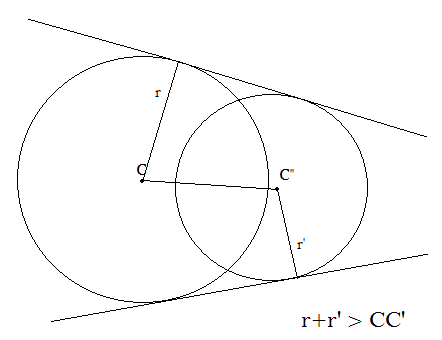
$ \Rightarrow {r_1} + {r_2} > 17$
On substituting the values we get,
$ \Rightarrow r + 4 > 17$
$ \Rightarrow r > 13$
∴ For r equal to 21, the number of common tangents is 2.
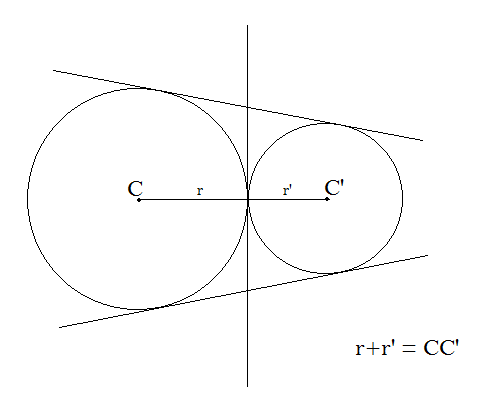
Again, the number of common tangents are 3 if and only if
${r_1} + {r_2} = 17$
On substituting the values we get,
$ \Rightarrow r + 4 = 17$
$ \Rightarrow r = 13$
∴ For r equal to 13, the number of common tangents is 3.
Therefore the correct options are (C) and (D).
Note: Note the 3 following cases:
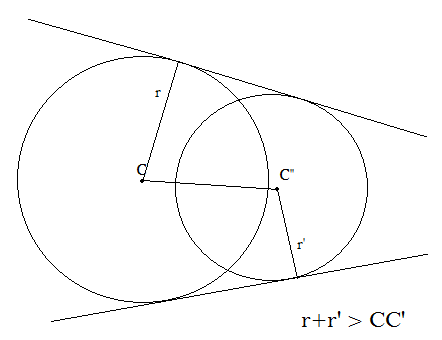
Case 1: If two circles intersect, then the sum of their radii must be greater than the distance between their centres. In that case, the number of common tangents will be 2.
Case 2: If two circles meet at a single point, then the sum of their radii must be equal to the distance between their centres. In that case, the number of common tangents is 3.
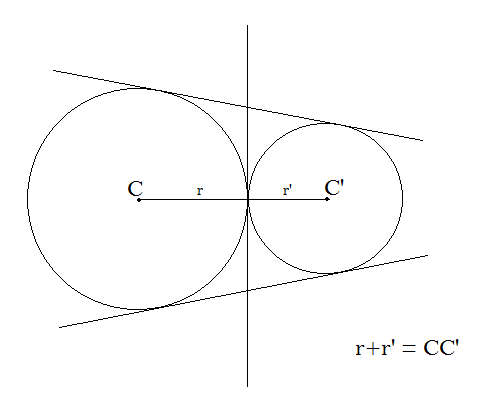
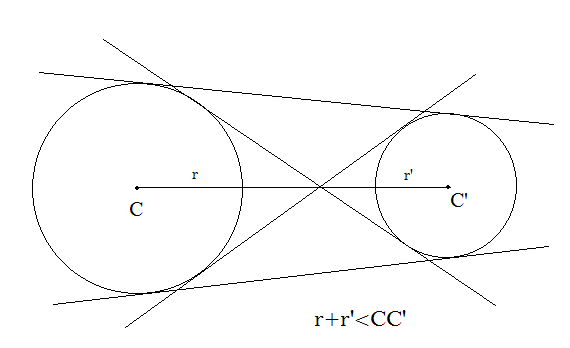
Case 3: If two circles neither meet nor intersect, then the sum of their radii must be less than the distance between their centres. In that case, the number of common tangents will be 4.
Complete step by step Answer:
We know that the general equation of a circle is given by $a{x^2} + b{y^2} + 2gx + 2fy + c = 0$ ,
∴ Its centre is located at\[ = ( - g,{\text{ }} - f)\]
And its radius is given by $ = \sqrt {{g^2} + {f^2} - c} {\text{ units}}$
Now, the equation of the first circle is given by ${x^2} + {y^2} - 10x + 16y + 89 - {r^2} = 0$
Therefore, its centre C1 is at \[(5, - 8)\]
And its radius r1 is given by
$ = \sqrt {{{(5)}^2} + {{\left( { - 8} \right)}^2} - \left( {89 - {r^2}} \right)} $
On simplification we get,
$ = \sqrt {25 + 64 - 89 + {r^2}} $
On adding first two terms and on simplification we get,
$ = r$units
Again, the equation of the second circle is given by ${x^2} + {y^2} + 6x - 14y + 42 = 0$
Therefore, its centre C2 is at \[( - 3,{\text{ }}7)\]
And its radius r2 is given by
$ = \sqrt {{{\left( { - 3} \right)}^2} + {{\left( 7 \right)}^2} - 42} $
On simplification we get,
$ = \sqrt {9 + 49 - 42} $
On adding the terms we get,
$ = \sqrt {16} $
On taking positive square root we get,
\[ = 4\] units
Now we know that the distance between the points (x1, y1) and (x2, y2) is given by
\[{\text{ }} = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \]
Therefore the distance between the centres of the two circles is
\[{C_1}{C_2} = \sqrt {{{\left( {5 + 3} \right)}^2} + {{\left( { - 8 - 7} \right)}^2}} \]
On simplification we get,
\[ = \sqrt {64 + 225} \]
On adding we get,
\[ = \sqrt {289} \]
On taking positive square root we get,
\[ = 17{\text{ }}\]units
Now, if these two circles intersect, therefore the sum of their radii must be greater than the distance between their centres. In that case the number of common tangents will be 2.

$ \Rightarrow {r_1} + {r_2} > 17$
On substituting the values we get,
$ \Rightarrow r + 4 > 17$
$ \Rightarrow r > 13$
∴ For r equal to 21, the number of common tangents is 2.
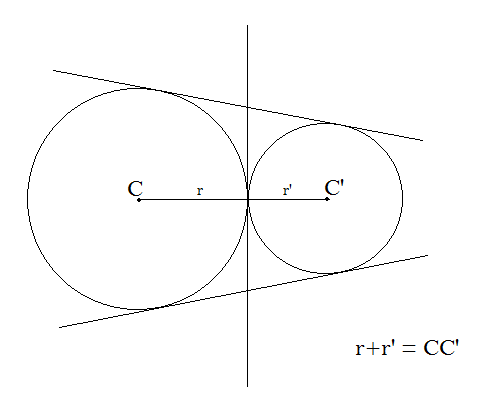
Again, the number of common tangents are 3 if and only if
${r_1} + {r_2} = 17$
On substituting the values we get,
$ \Rightarrow r + 4 = 17$
$ \Rightarrow r = 13$
∴ For r equal to 13, the number of common tangents is 3.
Therefore the correct options are (C) and (D).
Note: Note the 3 following cases:
Case 1: If two circles intersect, then the sum of their radii must be greater than the distance between their centres. In that case, the number of common tangents will be 2.

Case 2: If two circles meet at a single point, then the sum of their radii must be equal to the distance between their centres. In that case, the number of common tangents is 3.
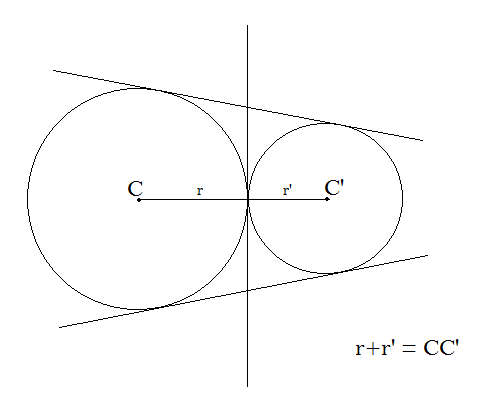
Case 3: If two circles neither meet nor intersect, then the sum of their radii must be less than the distance between their centres. In that case, the number of common tangents will be 4.

Recently Updated Pages
Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

The pH of the pancreatic juice is A 64 B 86 C 120 D class 12 biology CBSE

Explain sex determination in humans with the help of class 12 biology CBSE




