Question

For terrestrial magnetism establish a relation between the angle of dip $\theta $ horizontal component $H$ and vertical component $V$.

Answer 1

Hint: The angle that is made by the geomagnetic field with the horizontal in any place of the earth surface, is called the angle of dip or Dip.
Since the geomagnetic intensity is a vector quantity, this can be divided into two components i.e the horizontal component and the vertical component with the angle of dip.

Complete step by step answer:
The angle of dip: The angle that is made by the geomagnetic field with the horizontal in any place of the earth surface, is called the angle of dip or Dip.
If a bar magnet is hanged along its center of mass with the help of a thread freely it is shown that the magnetic axis makes an angle with the horizontal [fig-1]. The angle is the angle of dip. So if we know the angle of dip the direction of the geomagnetic field of any place can be found.

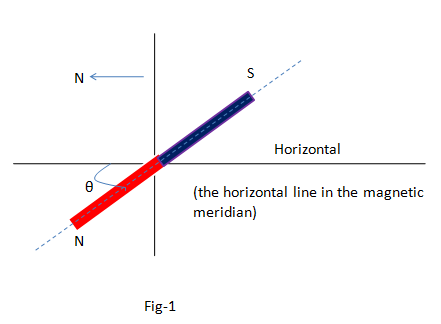
The geomagnetic intensity is a vector quantity. So it can be divided into two components along horizontal and vertical. Clearly, these two components are situated in the magnetic meridian.

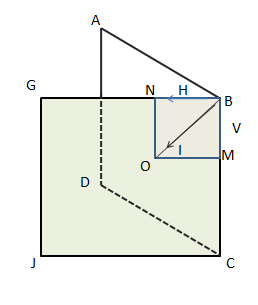
In the above figure $ABCD$ is the geographical meridian and $GBCJ$ is the magnetic meridian. At this point, $B$ the value and the direction of the geomagnetic intensity $I$ can be presented by $BO$ .
The horizontal component of the geomagnetic intensity $I$ is $H$. The value and the direction $H$ can be presented through $BN$.
The vertical component of the geomagnetic intensity $I$ is $V$. The value and the direction $V$ can be presented through $BM$.
Let the angle of dip is $\theta $,
$\therefore V = Isin\theta $ and $H = I\cos \theta $
$ \Rightarrow \dfrac{V}{H} = \dfrac{{Isin\theta }}{{I\cos \theta }}$
$ \Rightarrow \dfrac{V}{H} = \tan \theta $
This is the relation between the angle of dip, horizontal component, and vertical component.

Note:
• For a freely hanging magnet, the vertical plane that passes through the magnetic axis is called the magnetic meridian.
• And, the vertical plane that passes through the north and south poles of the earth of any place is called the geomagnetic meridian.
• The horizontal component of the geomagnetic intensity has not the same value everywhere on the earth's surface. At the Equator magnetic the value of the angle of dip $\theta = {0^ \circ }$ , so the value of $H = I$. This is the highest value of $H$. At the poles magnetic the value of the angle of dip $\theta = {90^ \circ }$ , so the value of $H = 0$. This is the lowest value of $H$. And at which place the value of the angle of dip $\theta = {45^ \circ }$, the horizontal component and vertical component are equal.