Question

For given figures find the value of x , where the diagonals are in terms of x.
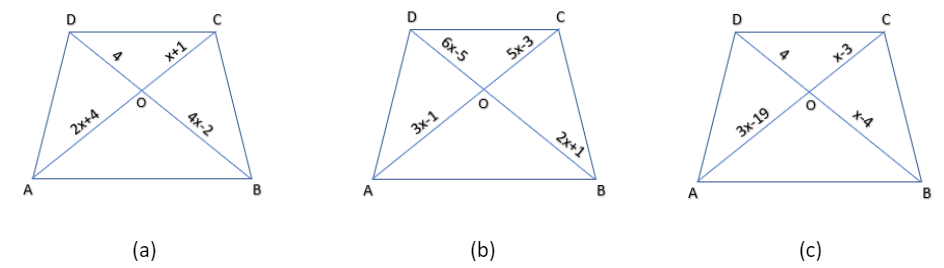
(i). In Fig. (a), \[AB\parallel CD,\] find the value of x.
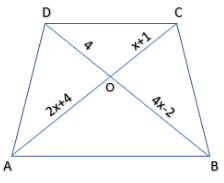
(ii). In Fig. (b), \[AB\parallel CD,\] find the value of x.
(iii). In Fig. (c), \[AB\parallel CD,\] if $OA = 3x - 19,OB = x - 4,OC = x - 3$ and $OD = 4,$ find x.

Answer 1

Hint- A quadrilateral with one pair of parallel sides is a trapezium. In each part of this question, the given 4-sided figure is a trapezium. Use the property of trapezium, diagonals of trapezium divide each other proportionally. Simply find the value of x by simplifying the equations so obtained.

Complete step-by-step solution -
(i) In fig (a), Given \[AB\parallel CD,\]
So, ABCD is a trapezium.
Since, diagonals of trapezium divide each other proportionally that’s why AC and BD divide each other proportionally.
$ \Rightarrow \dfrac{{AO}}{{CO}} = \dfrac{{BO}}{{DO}}$
Now, substitute the values of AO, CO, BO and DO

$ \Rightarrow \dfrac{{2x + 4}}{{x + 1}} = \dfrac{{4x - 2}}{4}$
On cross multiplying we get,
$ \Rightarrow 4(2x + 4) = (4x - 2)(x + 1)$
$ \Rightarrow 8x + 16 = 4{x^2} + 2x - 2$
$ \Rightarrow 0 = 4{x^2} + 2x - 8x - 2 - 16$
$ \Rightarrow 0 = 4{x^2} - 6x - 18$
or, $4{x^2} - 6x - 18 = 0$ …………………………. (a)
$ \Rightarrow (x - 3)(2x + 3) = 0$
$\therefore $ $x = 3$ or $x = \dfrac{{ - 3}}{2}$
Hence, the value of x = 3 or $x = \dfrac{{ - 3}}{2}$

(ii) In fig (b), Given \[AB\parallel CD,\]

So, ABCD is a trapezium.
Since, diagonals of trapezium divide each other proportionally that’s why AC and BD divide each other proportionally.
$ \Rightarrow \dfrac{{AO}}{{CO}} = \dfrac{{BO}}{{DO}}$
Now, substitute the values of AO, CO, BO and DO
$ \Rightarrow \dfrac{{3x - 1}}{{5x - 3}} = \dfrac{{2x + 1}}{{6x - 5}}$
On cross multiplying we get,
$ \Rightarrow (6x - 5)(3x - 1) = (2x + 1)(5x - 3)$
$ \Rightarrow 18{x^2} - 21x + 5 = 10{x^2} - x - 3$
$ \Rightarrow 18{x^2} - 10{x^2} - 21x + x + 5 + 3 = 0$
$ \Rightarrow 8{x^2} - 20x + 8 = 0$
or, $2{x^2} - 5x + 2 = 0$ ………………………….. (b)
$ \Rightarrow (x - 2)(2x - 1) = 0$
$\therefore $ $x = 2$ or $x = \dfrac{1}{2}$
Hence, the value of x = 2 or $x = \dfrac{1}{2}$

(iii) In fig (c), Given \[AB\parallel CD,\]

So, ABCD is a trapezium.
Since, diagonals of trapezium divide each other proportionally that’s why AC and BD divide each other proportionally.
$ \Rightarrow \dfrac{{AO}}{{CO}} = \dfrac{{BO}}{{DO}}$
Now, substitute the values of AO, CO, BO and DO
$ \Rightarrow \dfrac{{3x - 19}}{{x - 3}} = \dfrac{{x - 4}}{4}$
On cross multiplying we get,
$ \Rightarrow 4 \times (3x - 19) = (x - 4)(x - 3)$
$ \Rightarrow 12x - 76 = {x^2} - 7x + 12$
$ \Rightarrow {x^2} - 19x + 88 = 0$
$ \Rightarrow (x - 8)(x - 11) = 0$ ……………………………….. (c)
$\therefore $ $x = 8$ or $x = 11$
Hence, the value of x = 8 or $x = 11$

Note- In such types of questions, just keep in mind the basic proportionality of diagonal components in a trapezium and also solving the quadratic equation so obtained by using the splitting the middle term method, completing the square method or discriminant method.