Question

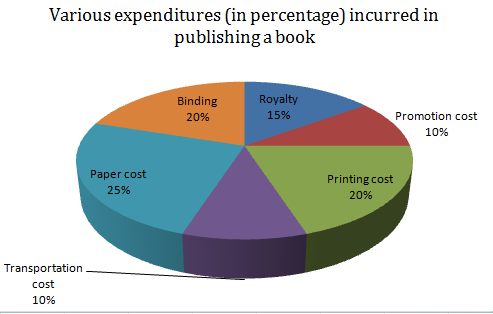
For an edition of 12,500 copies, the amount of Royalty paid by the publisher is Rs. 2,81,250. What would be the selling price of the book if the publisher desires a profit of $5\%$.

(a) Rs. 152.50
(b) Rs. 157.50
(c) Rs. 162.50
(d) Rs. 167.50

Answer 1

Hint: It is given that the publisher desires a profit of $5\%$ so the selling price of the book is $105\%$ of the cost price of the book. Now, let us assume the selling price of 12,500 books is x. And we know the amount of Royalty that publishers pay and the percentage contribution of it in total expenditure along with that we know the selling price for 12,500 copies so the ratio of 15 to 105 is equal to the ratio of 2,81,250 to x. Solve this ratio expression and get the value of x. Now, x is the selling price for 12,500 books so the selling price for 1 book is equal to the division of x divided by 12,500.

Complete step by step answer:
In the above problem, a profit of $5\%$ is given on selling a book. So, the relationship between cost price and selling price is equal to:
$S.P.=C.P.\left( 1+\dfrac{\text{Profit}}{100} \right)$
Substituting the value of profit as $5\%$ in the above equation we get,
$\begin{align}
  & S.P.=C.P.\left( 1+\dfrac{5}{100} \right) \\
 & \Rightarrow S.P.=C.P.\left( \dfrac{100+5}{100} \right) \\
 & \Rightarrow S.P.=C.P.\left( \dfrac{105}{100} \right) \\
\end{align}$
From the above formula, we can say that the selling price of a book is equal to $105\%$ of cost.
Let us assume that the selling price of 12500 books is x.
Now, we have given the royalty paid by the publisher is equal to Rs. 2,81,250 and the percentage of royalty with respect to the cost price of a book is given as $15\%$ so we can write the relationship between royalty and selling price of the book as follows:
$\dfrac{15}{105}=\dfrac{281250}{x}$
Cross multiplying the above equation we get,
$\begin{align}
  & 15x=105\left( 281250 \right) \\
 & \Rightarrow 15x=29531250 \\
 & \Rightarrow x=\dfrac{29531250}{15}=1968750 \\
\end{align}$
This is the selling price for 12500 books so to find the selling price of 1 book we are going to divide 1968750 by 12500.
$\begin{align}
  & \dfrac{1968750}{12500} \\
 & =157.50 \\
\end{align}$
From the above solution, we got the selling price for a book as Rs. 157.50.

So, the correct answer is “Option B”.

Note: The mistake that you could make in this problem is that it has written above the pie chart that these are the percentages of expenditures incurred on a book so don’t confuse that the percentages of expenditure are incurred on 12500 copies of a book. Also, make sure while doing the calculations because the figures we are dealing with are large so you might mess up the calculation.