Question

For a regular polygon, let r and R be the radii of the inscribed and the circumscribed circles. Which of the following is the false statement?
(A) There is a polygon with \[\dfrac{r}{R} = \dfrac{1}{{\sqrt 2 }}\]
(B) There is a polygon with \[\dfrac{r}{R} = \dfrac{2}{3}\]
(C) There is a polygon with \[\dfrac{r}{R} = \dfrac{{\sqrt 3 }}{2}\]
(D) There is a polygon with \[\dfrac{r}{R} = \dfrac{1}{2}\]

Answer 1

Hint: Draw a diagram of a regular polygon according to the question. Now find a right-angled triangle with sides as $'R'$ and $'r'$. Form a general relation for the ratio of $'r'$ and $'R'$ as given in the options. Now find out which of the values given in options are possible for whole number values of $n$.

Complete step-by-step answer:

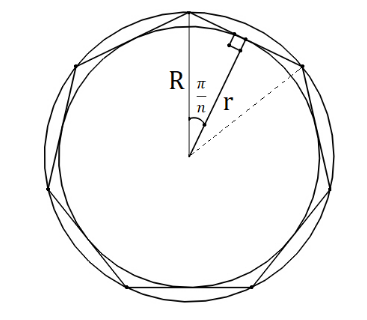
According to the question $'r'$ is the radius of the inscribed circle and $'R'$ is the radius of the circumscribed circle. Now let’s take any regular polygon with ($'n'$ sides) an inscribed circle and circumscribed circle. Notice, using a figure, if you join the vertices of the polygon to the common centre point, then you will see that the whole angle is divided into equal parts which are equal to the number of sides of the polygon, i.e. $2\pi $ is divided equally into $n$ parts. So, each of these angles will be$\dfrac{{2\pi }}{n}$.
Now join the midpoint of a side, which is also the point of contact for the inscribed circle, to the common centre. Hence, the angle $\dfrac{{2\pi }}{n}$is further divided into two equal parts, i.e. $\dfrac{{2\pi }}{n} \times \dfrac{1}{2} = \dfrac{\pi }{n}$. Therefore, we get a right-angled triangle with its one arm as $'r'$and hypotenuse as$'R'$.
$ \Rightarrow \cos \dfrac{\pi }{n} = \dfrac{r}{R}$ ; where $n$ is the number of sides of the polygon and is valid for any regular polygon.
Since, we have to find the false statement among the given option, let’s check our options:
For$n = 4$, which is a square, we have:
$ \Rightarrow \dfrac{r}{R} = \cos \dfrac{\pi }{4} = \dfrac{1}{{\sqrt 2 }}$
For$n = 3$, which is an equilateral triangle, we have:
$ \Rightarrow \dfrac{r}{R} = \cos \dfrac{\pi }{3} = \dfrac{1}{2}$
For$n = 6$, which is a regular hexagon, we have:
$ \Rightarrow \dfrac{r}{R} = \cos \dfrac{\pi }{6} = \dfrac{{\sqrt 3 }}{2}$
So, we got the statements (A), (C) and (D) as one of the possible solutions. But according to option (B), the solution is \[\dfrac{r}{R} = \dfrac{2}{3}\]
$ \Rightarrow \dfrac{r}{R} = \dfrac{2}{3} = \cos \dfrac{\pi }{n}$
And since we know $\dfrac{1}{2} < \dfrac{2}{3} < \dfrac{1}{{\sqrt 2 }} \Rightarrow \cos \dfrac{\pi }{3} < \cos \dfrac{\pi }{n} < \cos \dfrac{\pi }{4}$
This implies that $n$ must lie between $3$ and $4$, which is not possible for a whole number.

Therefore, the option (B) is a false statement.

Note: Try to understand the diagram well while going through the solution. Since we have to find the false statement from the options given so we have to go by checking from the options after finding the relation. An alternative approach for this problem is to check for whether $\cos \dfrac{\pi }{n} = \dfrac{r}{R}$ attains the given values for any $n$ as a natural number.