Question

For a first-order reaction:
$A(g)\rightleftharpoons 3B(g)$
The concentration versus time graph is given below:

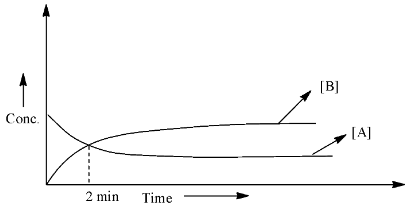
What is the half-life in minutes (answer to the nearest integer)?

Answer 1

Hint: Half-life is the time when the concentration of the reactant becomes half of the concentration taken at the starting of the reaction. From the graph, we can calculate the half-life when the concentration of the reactant is equal to the concentration of the product.

Complete answer: The given reaction is:
$A(g)\rightleftharpoons 3B(g)$
And the question says that this reaction is first order, which means that the rate of the reaction depends only on the concentration of one reactant.
Half-life is the time when the concentration of the reactant becomes half of the concentration taken at the starting of the reaction. From the graph, we can calculate the half-life when the concentration of the reactant is equal to the concentration of the product.
So, the given graph is:

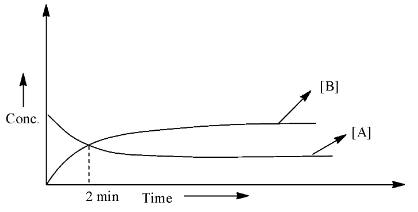
As we can see that the starting concentration of A is the highest and the concentration of B is zero. After 2 minutes, both the lines meet, which means that the concentration of the reactant and the product is equal. Therefore, half of the concentration of the A has been converted into a product, hence, this should be the half-life for the reaction.
Therefore, the half-life of the reaction is 2 min and this answer is already in the form of an integer.

Note: If the graph is not given for a reaction, but the rate constant, i.e., k is given for any first-order reaction, then we can calculate the half-life of the reaction by using the formula:
${{t}_{1/2}}=\dfrac{0693}{k}$