Question

For a closed (not rigid ) container containing $n = 10$ moles of an ideal gas fitted with a movable, frictionless, weightless piston operating such that pressure of gas remains constant at $0.821atm$.Which graph represents a correct variation of log V vs log T where V is in litre and T in Kelvin?
A)
 

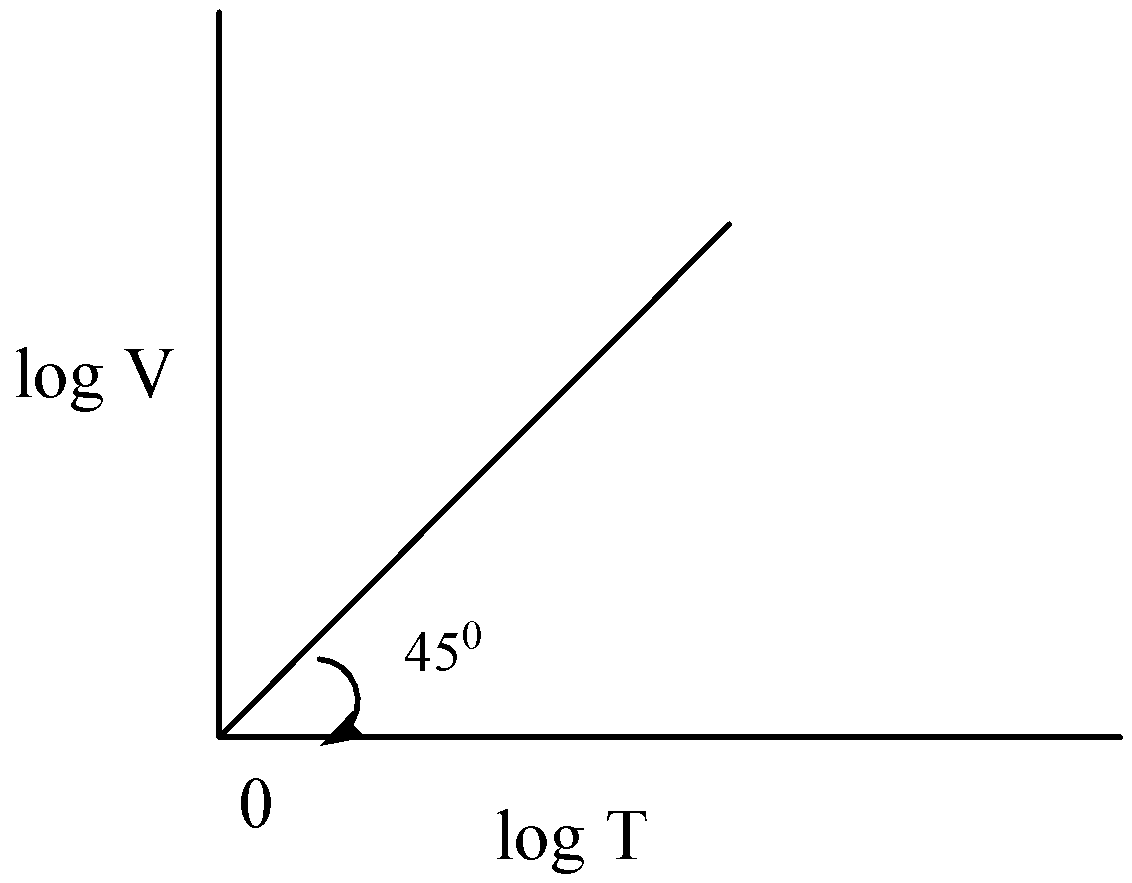
B)
  

C)
 

D)

Answer 1

Hint:We know that the ideal gas law is the condition of a speculative ideal gas. It is a decent estimation of the conduct of numerous gases under numerous conditions, despite the fact that it has a few impediments
The ideal gas equation is,
$PV = nRT$
Where P is the pressure in the atmosphere.
V is the volume of gas in a liter.
n is the number of moles.
R is a universal gas constant.
T is the temperature.

Complete step by step answer:
Given,
The number of moles $n = 10$.
The pressure of gas is $0.821atm$.
The value of gas constant is $0.0821Latmmo{l^{ - 1}}{K^{ - 1}}$.
We know the ideal gas equation is,
$PV = nRT$
Now, substitute the known qualities in the above condition,
$V = \dfrac{{10 \times 0.0821 \times T}}{{0.821}}$
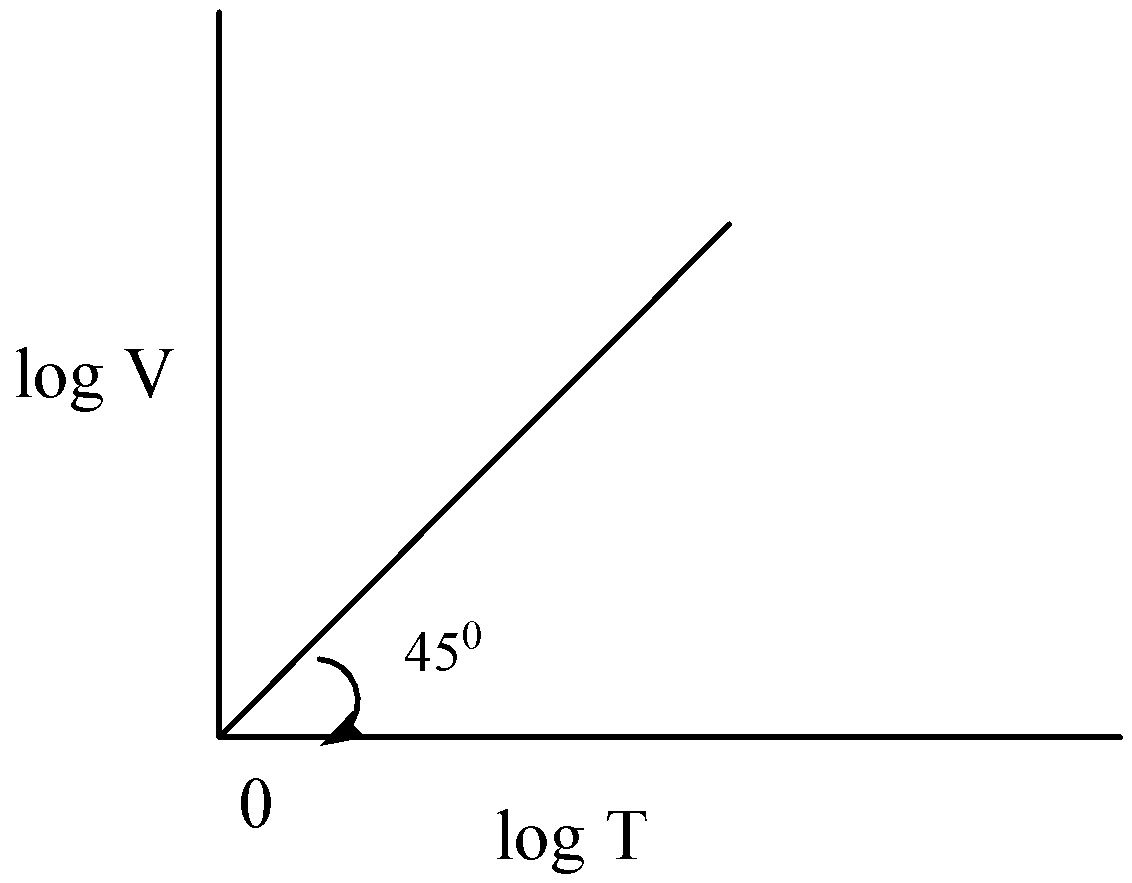
$V = 1 \times T$
$\dfrac{{\log V}}{{\log T}} = 1$
$\tan \theta = 1$
$\tan {45^ \circ } = 1$
Hence option A is correct.

Additional information:
If the gas obeys an ideal gas equation then the pressure is given by,
${\text{P = }}\dfrac{{{\text{nRT}}}}{{\text{V}}} \to 1$
If the volume is doubled and the temperature is halved then the equation becomes,
${\text{P = }}\dfrac{{{\text{nRT/2}}}}{{{\text{2V}}}}$
${\text{P = }}\dfrac{{{\text{nRT}}}}{{{\text{4V}}}} \to 2$
From equation 1 ${\text{P = }}\dfrac{{{\text{nRT}}}}{{\text{V}}}$ then the equation 2 becomes,
${\text{P = }}\dfrac{{\text{P}}}{{\text{4}}}$
Thus, if the volume is doubled and the temperature is halved then the pressure of the system decreases by four times.

Note:
We know that,
${\text{Density}}{\text{ = }}\dfrac{{{\text{mass}}}}{{{\text{volume}}}}$
Assuming mass is equal to the number of moles in ideal gas.
${\text{Density = }}\dfrac{{\text{n}}}{{{\text{volume}}}}$
The ideal gas equation is,
${\text{PV = nRT}}$
The number of moles can be calculated as,
${\text{n = }}\dfrac{{{\text{PV}}}}{{{\text{RT}}}}$
Substituting the value of n in density equation,
\[{\text{Density = }}\dfrac{{P\not V}}{{RT\not V}}\]
\[{\text{Density = }}\dfrac{{\text{P}}}{{{\text{RT}}}}\]
\[{\text{Density}} \propto \dfrac{{\text{1}}}{{\text{T}}}\]
It is clear that density is inversely proportional to temperature. Thus, as the density of the gas decreases temperature increases.