Question

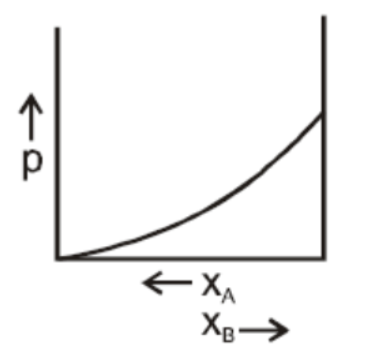
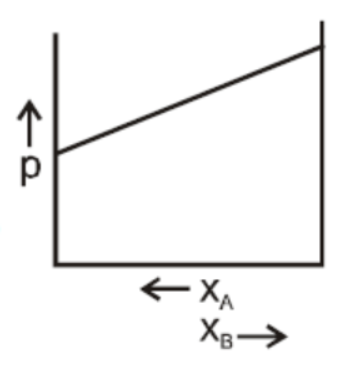
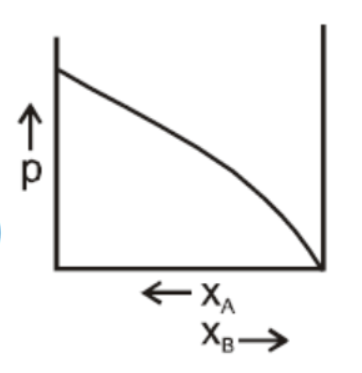
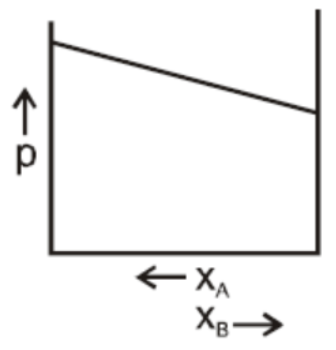
For a binary ideal liquid solution, the variation in total vapour pressure versus composition of the solution is given by which of the curves?
A.

B.

C.

D.

Answer 1

Hint:As known, a binary liquid solution is a mixture of two liquids which are completely miscible with one and another. Their boiling point usually depends upon the solution composition.

Complete step by step answer:
Now in this question,
In a binary ideal liquid solution, the variation in total vapour pressure versus composition of the solution is given by the graphs in B and D in which the total vapour pressure shows a linear composition of the solution.
As the mole fraction of more volatile components increases, the total vapour pressure increases.
We can explain this by as, the dependency on the vapour pressure of the pure component A and B, the total vapour pressure over the solution either decreases or increases as of with the increase of the mole fraction of component A.
And hence option A is the correct answer.

Additional information
For the dependency of the boiling points of the binary solutions, there can be three cases of such - The boiling points of solutions of all compositions lie between the boiling points of clean liquids.the boiling points of solutions of any composition lies above the boiling points of clean liquids and the boiling points of solutions of some compositions lies below the boiling points of clean liquids

Note:
Keep in mind that the total vapour pressure is the overall vapour pressure present in an equilibrium state, such that it is the summation of partial vapour pressure of the components A and B. The vapour pressure is that, of a single component in a mixture contributes to the total pressure in the system called partial pressure.