Question

What is the focal length of double concave lens kept in air with two spherical surface of radii ${{R}_{1}}=30cm$ and ${{R}_{2}}=60cm$. Take the refractive index of the lens as $\mu =1.5$.

Answer 1

- Hint: A double concave lens is nothing but a biconcave lens in which both the surfaces of the lens are concave in nature. Focal length of a lens is the distance between the centre of the lens and the focus. Focal length of a lens can be calculated using lens makers formula. Since thickness of the lens is not given in the question, a simplified version of lens makers formula can be used to determine the focal length.

Complete step-by-step solution
A double concave lens has two concave surfaces on both the ends. When light from an object is made to pass through a double concave lens from one of the sides of the lens, a virtual image is formed on the same side of the lens. A double concave lens acts as a diverging lens.
Let us assume that the concave surface which is close to the light source has a radius ${{R}_{1}}$ and the concave surface away from the light source has a radius ${{R}_{2}}$. To find the focal length of a double concave lens, let us proceed by applying the lens maker formula. Lens makers formula is given by
$\dfrac{1}{f}=(\mu -1)\left[ \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right]$
where
$f$ is the focal length of the double concave lens.
$\mu $ is the refractive index of the lens
${{R}_{1}}$ is the radius of the concave surface close to the light source
${{R}_{2}}$ is the radius of the concave surface away from the light source.
Let this be equation 1.
Let us assume ${{R}_{1}}$ to be $30cm$ and ${{R}_{2}}$ to be $60cm$, as provided in the question. We are also given that $\mu =1.5$. Substituting these values in equation 1, we have
$\dfrac{1}{f}=(\mu -1)\left[ \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right]=(1.5-1)\left[ \dfrac{1}{(-30)}-\dfrac{1}{60} \right]=(0.5)\left[ \frac{-3}{60} \right]=(0.5)\left[ \dfrac{-1}{20} \right]\Rightarrow f=\left[ \dfrac{-20}{0.5} \right]=-40cm$
Therefore, the focal length of the given double concave lens is equal to $40cm$.
It is important to note that the lens maker's formula follows sign convention. In this case, the focal length of the double concave lens turns out to be a negative value. This suggests that a virtual image of the object is formed on the same side of the lens. Also note that we considered one of the radii of the biconcave lens to be negative. Here, in this solution, the radius of the concave surface close to the light source is taken as negative and the radius of the concave surface away from the light source is taken as positive, as shown in the following ray diagram of a concave lens.

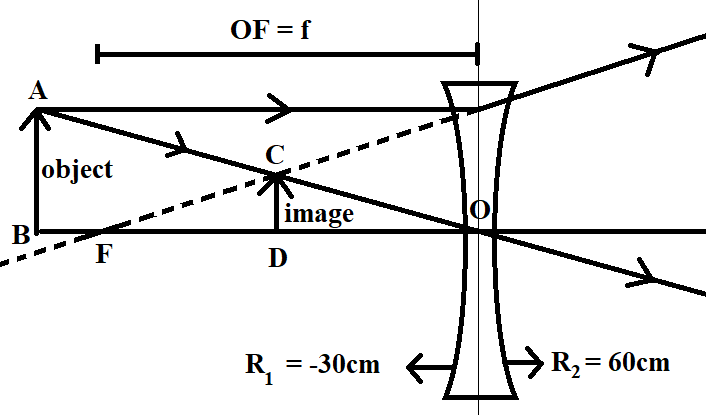
In this ray diagram, we have considered the radius of curvature of the lens close to the light source $({{R}_{1}})$ as negative and radius of curvature of the lens away from the light source $({{R}_{2}})$ as positive. It can be seen that the image $(CD)$ formed is virtual, on the same of the lens, where the object $(AB)$ is placed. Also to be noted that the focal length $(f)$ is equal to the distance between the focus $(F)$ and the centre of the lens $(O)$.

Note: Lens makers formula is also dependent on the thickness of the lens $d$ as given in the following formula.
$\dfrac{1}{f}=(\mu -1)\left[ \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}}+\dfrac{(\mu -1)d}{\mu {{R}_{1}}{{R}_{2}}} \right]$
But here, in this question, we are not provided with the thickness of the lens. So, we assume the lens to be a thin lens and carry out thin lens approximation to the lens makers formula.