Question

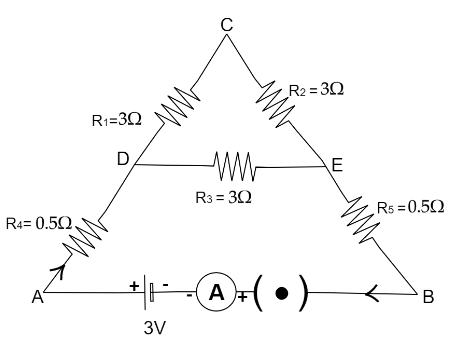
Five resistors are connected in a circuit as shown below. Find the ammeter reading when the circuit is closed.

Answer 1

Hint:We have to solve this complicated circuit into a simplified one to get the current flowing through the ammeter. First solve the total resistance between DCE then calculate the total resistance between D and E, finally we can calculate the equivalent resistance and now with help of ohm’s law we can calculate the ammeter reading.

Complete step by step answer:
We have five resistance and are connected as shown below,

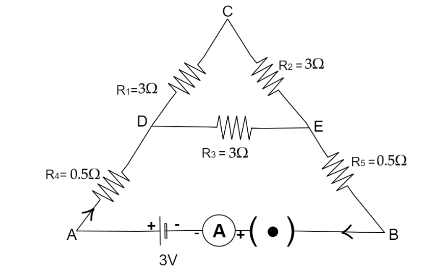
Now from the diagram we can see that resistance $R_1\,\,and\,R_2$ are connected in series in branch DCE,
$R_{12} = R_1 + R_2$
Now putting the known value we will get,
$R_{12} = 3\Omega + 3\Omega $
$ \Rightarrow R_{12} = 6\Omega $

Now the equivalent circuit will look like,

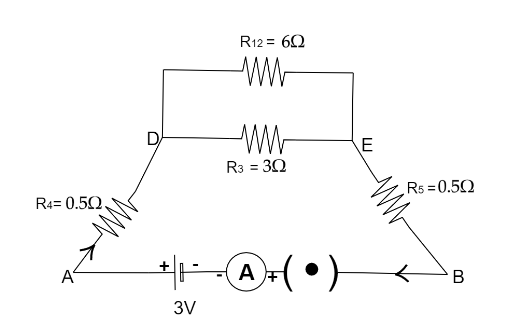
Now $R_{12}\,\,{\text{and}}\,R_3$ resistance are connected parallel in branch DE,
$R_{DE} = R_{12}||\,R_3$
We know, $R = Ra||\,Rb = \dfrac{{Ra \times Rb}}{{Ra + Rb}}$
Now applying this formula in the above DE branch we will get,
$R_{DE} = \dfrac{{R_{12} \times \,R_3}}{{R_{12} + R_3}}$
Now putting the known value we will get,
$R_{DE} = \dfrac{{6\Omega \times \,3\Omega }}{{6\Omega + 3\Omega }}$
$ \Rightarrow R_{DE} = \dfrac{{18\Omega }}{9}$
Dividing the numerator and denominator by $9$ we will get,
$R_{DE} = 2\Omega $

Now the equivalent resistance will be,

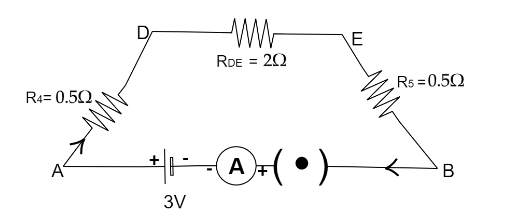
Now the equivalent resistance, from the above diagram $R_4,R5\,{\text{and}}\,R_{DE}$ are connected in series. We will get,
$\operatorname{R} {\text{eq = R_4 + }}R_{DE} + R5$
Putting the known values in the above equation we will get,
$\operatorname{R} {\text{eq = 0}}{\text{.5}}\Omega {\text{ + }}2\Omega + 0.5\Omega $
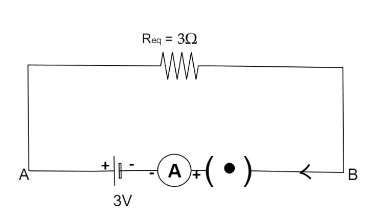
$ \Rightarrow \operatorname{R} {\text{eq = }}3\Omega $
Hence the equivalent resistance of the circuit is $3\Omega $.

Ammeter: It is an instrument for measuring either direct or alternating electric current, in amperes.
For Ammeter Reading, applying Ohm’s Law we will get,
$I = \dfrac{V}{R}$
Now putting the known value from the diagram we will get,
$I = \dfrac{{3V}}{{3\Omega }}$
$ \therefore I = 1A$

Hence the current reading in ammeter is $1\,A$.

Note: Also while solving this kind of problem always draw the simplified circuit in each step so that you will not commit a mistake. We can solve this problem in many different ways. We can use the delta star method to open the circuit in a simplified version but for now we only know the envelope theory. In future classes you will come to know many other simplified methods to solve this kind of complicated circuit.