Question

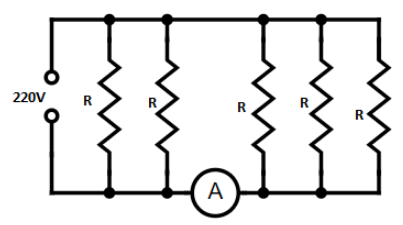
Five identical lamps each resistance $R = 1100\Omega $ are connected to $220V$ as shown in figure. The reading of ideal ammeter A is

A. $\dfrac{1}{5}\,amp$
B. $\dfrac{2}{5}\,amp$
C. $\dfrac{3}{5}\,amp$
D. $1\,amp$

Answer 1

Hint: Above diagram represents some resistance along with some voltage and ammeter. There are five lamps of resistance in series and for this resistance there is some ohm value and there is voltage value also. Considering those values we are going to solve this with the help of ohm's law.

Complete step by step answer:
Five identical lamps have five resistances and for those five resistances there is some current flowing through the ammeter and there is some voltage value also there. Here current is flowing in the above diagram that means, $I = {I_1} = {I_2} = {I_3} = {I_4} = {I_5}$ equal current is passing in above diagram.
By applying ohm's law, $V = IR$
Here voltage, $V = 220V$
Resistance, $R = 1100\Omega $
Therefore, $I = \dfrac{V}{R}$

By substituting resistance and voltage current values in current we get,
$I = \dfrac{{220}}{{1100}} \\
\Rightarrow I = \dfrac{1}{5} \\ $
Now we are going to calculate the current in ammeter
That means, ${I_A} = {I_3} + {I_4} + {I_5}$
Already we have concluded the current in beginning only, then
${I_A} = I + I + I \\
\Rightarrow {I_A} = 3I \\ $
We have calculated the current value by using ohm's law, so
$\therefore {I_A} = 3 \times \dfrac{1}{5}$
So the current in ammeter is, ${I_A} = \dfrac{3}{5}\,amp$

Thus the correct option is C.

Note: From the beginning of the solution part we have clearly shown, for finding the current in ammeter we are using ohm's law. Using ohm's law we have found the current value with given resistance and voltage values. We have considered equal current is passing throughout the circuit, on this base only we have found the current in ammeter.