Question

Five coplanar forces (each of magnitude 20N) are acting on a body. The angle between two neighboring forces has the same value. The resultant of these forces is necessarily equal to
(A) $20N$
(B) $20\sqrt 2 $N
(C) Zero
(D) None of These

Answer 1

Hint:If in an n-sided polygon, all the sides denote vectors in order (i.e. the next vector starts from the head of the previous vector) then the resultant is zero. Here we have 5 vectors and they are at equal angles from each other, i.e. they are at angle $72^\circ$ from each other, if we try to rearrange these vectors, we can rearrange them in the form of a polygon.

Complete step by step answer:
The forces given in the question are of the following form. The angle between any two consecutive forces is $72^\circ$.

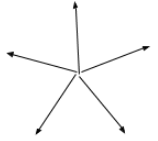
If we rearrange these forces and try to arrange them in order, then we will get

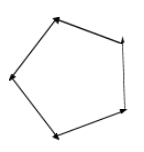
Since on rearrangement the forces are forming a polygon, the resultant of these forces must be zero.Therefore, the correct answer to the question is option : C

Note: Alternatively, the situation given in the question can also be studied by taking fewer numbers of vectors. First, consider that there are 2 vectors and they are acting at the same point and they are such that all consecutive angles are equal then the two forces will be at angle 180$^{\circ}$ from each other and they will cancel each other so the resultant will be zero. Now, consider that there are 3 vectors and they are acting at the same point and they are such that all consecutive angles are equal then the two forces will be at angle 120$^{\circ}$ from each other and we know that if three equal vectors are at 120$^{\circ}$ from each other the resultant will be zero. Now, consider that there are 4 vectors and they are acting at the same point and they are such that all consecutive angles are equal then the two forces will be at angle 90$^{\circ}$ from each other and we can easily see that there will be two pairs of equal vectors opposite from each other and hence the resultant will again be zero. Similarly, we can say that if there are n number of vectors and they are acting at the same point such that all consecutive angles are equal then their resultant will be zero.