Question

Find x such that the four points $A(4,4,4),\,B(5,x,8),\,C(5,4,1){\text{ and }}D(7,7,2)$ are coplanar.

Answer 1

Hint: If the points or the lines are lying on the same plane then, they are known to be coplanar. In other words, a group of points or the lines are said to be coplanar if, they are creating or occupying zero volume in space that means, when the endpoints are joined then they have only two dimensions in space out of length, width, and height and so we can say that coplanar points are always available in a two-dimensional plane.

Mathematically, for the coplanar points or lines, the triple product is always zero. In this question, we have already been given that the points $A(4,4,4),\,B(5,x,8),\,C(5,4,1){\text{ and }}D(7,7,2)$ are coplanar and so, we have to get the triple product as zero to determine the value of x.
To start solving the question, first, find the distance of the line segments joined to a common point and carry out the triple product calculation.

Complete step by step answer:
Let all the four points are connected with the origin in a way that the distance of the points from the origin is:

\[
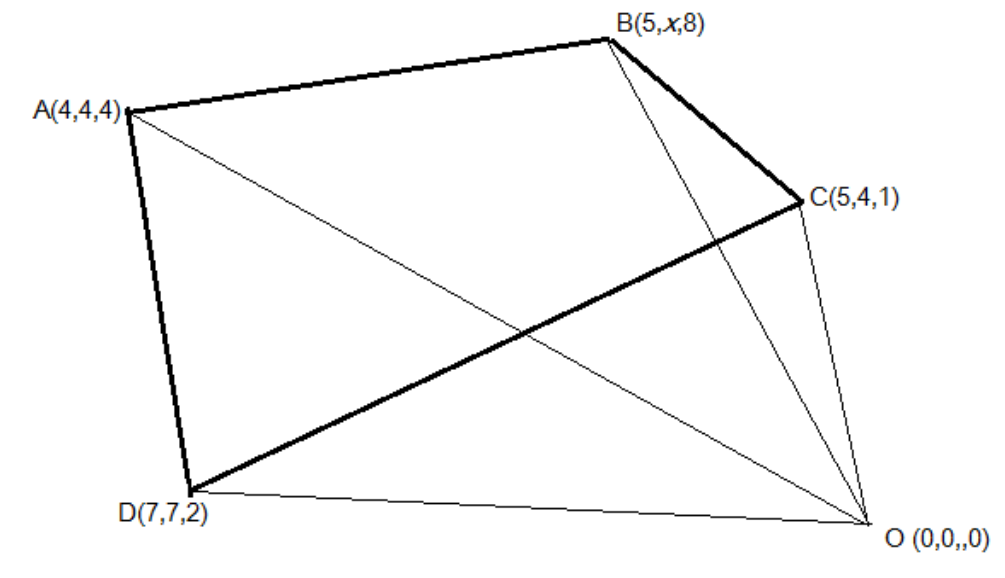
  OA = 4\hat i + 4\hat j + 4\hat k \\
  OB = 5\hat i + x\hat j + 8\hat k \\
  OC = 5\hat i + 4\hat j + \hat k \\
  OD = 7\hat i + 7\hat j + 2\hat k \\
 \]
Now, the distance between the points can be calculated as:
$
  AB = OB - OA \\
   = 5\hat i + x\hat j + 8\hat k - 4\hat i - 4\hat j - 4\hat k \\
   = \hat i + (x - 4)\hat j + 4\hat k \\
  AC = OC - OA \\
   = 5\hat i + 4\hat j + \hat k - 4\hat i - 4\hat j - 4\hat k \\
   = \hat i - 3\hat k \\
  AD = OD - OA \\
   = 7\hat i + 7\hat j + 2\hat k - 4\hat i - 4\hat j - 4\hat k \\
   = 3\hat i + 3\hat j - 2\hat k \\
 $

Now, as all the points are coplanar so, the triple product of the line segments $AB,\,AC,\,AD$ is zero.

$
  |AB,AC,AD| = 0 \\
  \left| {\begin{array}{*{20}{c}}
  1&{x - 4}&4 \\
  1&0&{ - 3} \\
  3&3&{ - 2}
\end{array}} \right| = 0 \\
= 1(0 + 9) - (x - 4)( - 2 + 9) + 4(3) = 0 \\
= 9 - 7(x - 4) + 12 = 0 \\
= 9 - 7x + 28 + 12 = 0 \\
= 7x = 49 \\
= x = 7 \\
 $

Hence, the value of x is 7 such that the four points $A(4,4,4),\,B(5,x,8),\,C(5,4,1){\text{ and }}D(7,7,2)$ are coplanar.

Note: To determine the length of the line segment joining two points, we need to determine the distance between the points by using the formula \[AB = \left( {{a_1} - {b_1}} \right)\hat i + \left( {{a_2} - {b_2}} \right)\hat j + \left( {{a_3} - {b_3}} \right)\hat k\] where, $A = {a_1}\hat i + {a_2}\hat j + {a_3}\hat k$ and, $B = {b_1}\hat i + {b_2}\hat j + {b_3}\hat k$.
It is always advised to the candidates to follow the same formula throughout the question to avoid any sort of error.