Question

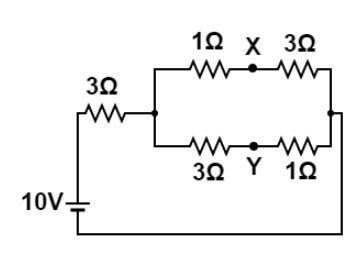
Find ${V_{XY}}$.

Answer 1

Hint: In order to solve this question we need to understand the resistance and resistance combination. Resistance is defined as opposition offered by wire when a current is passed through it, actually when a current is passed through wire then wire opposes the state change and hence develops resistance. Two different resistance combinations, one is a series and the other is a parallel combination. In series combination current through all resistors is the same and voltage varies in ratio of resistance whereas in parallel combination voltage through each resistance is same and current varies in inverse ratio of their resistance.

Formula used:
For a series resistance, let resistance ${R_1},{R_2},{R_{3,}}{R_{4,}}.........{R_n}$ resistances are connected in series with each other.So equivalent resistance is given by,
$R = \sum\nolimits_{i = 1}^n {{R_i}} $
Voltage across each resistance is defined as,
${V_i} = \dfrac{{V{R_i}}}{{\sum\nolimits_{i = 1}^n {{R_i}} }}$ here, $i = 1,2,3,.......n$
For a parallel resistance, let resistance ${R_1},{R_2},{R_{3,}}{R_{4,}}.........{R_n}$ resistances are connected in parallel with other.So equivalent resistance is given by,
$\dfrac{1}{R} = \sum\nolimits_{i = 1}^n {\dfrac{1}{{{R_i}}}} $

Complete step by step answer:
So first we simplify the given circuit, since in X arm resistances are in series with each other, so by using formula of series resistance we get, equivalent resistance in X arm is,
${R_1} = 1\Omega + 3\Omega $
$\Rightarrow {R_1} = 4\Omega $
Similarly, in Y arm resistances are in series with each other, so by using formula of series resistance we get, equivalent resistance in Y arm is,
${R_2} = 1\Omega + 3\Omega $
$\Rightarrow {R_2} = 4\Omega $
Since both ${R_1}\& {R_2}$ are in parallel with each other so equivalent resistance is given by,
$\dfrac{1}{{{R_3}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$
$\Rightarrow {R_3} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}$
$\Rightarrow {R_3} = \dfrac{{4 \times 4}}{{4 + 4}}$
$\Rightarrow {R_3} = \dfrac{{16}}{8}$
$\Rightarrow {R_3} = 2\Omega $

Now resistance ${R_3}\& 3\Omega $ are in series with each other so voltage across ${R_3}$ is calculated using voltage division of series resistance we get, ${V_1} = \dfrac{{V{R_3}}}{{{R_3} + 3\Omega }}$
From circuit, $V = 10Volt$
So, ${V_1} = \dfrac{{10 \times 2}}{{2 + 3}}$
${V_1} = \dfrac{{20}}{5}volt$
$\Rightarrow {V_1} = 4\,Volt$
So Voltage across both arms X and Y is ${V_1} = 4\,Volt$
Let the voltage at X be ${V_X}$
So in X arm, voltage across $1\Omega $ is given by, ${V_2} = \dfrac{{{V_1} \times 1\Omega }}{{1\Omega + 3\Omega }}$
Putting values we get, ${V_2} = \dfrac{{4 \times 1}}{4}$
${V_2} = 1\,Volt$
Since, ${V_2} = {V_1} - {V_X}$
Putting values we get, ${V_X} = {V_1} - {V_2}$
${V_X} = 4 - 1$
$\Rightarrow {V_X} = 3\,Volt$

Similarly in armY, Let the voltage at Y be ${V_Y}$.So in Y arm, voltage across $3\Omega $ is given by, ${V_3} = \dfrac{{{V_1} \times 3\Omega }}{{1\Omega + 3\Omega }}$
Putting values we get, ${V_3} = \dfrac{{4 \times 3}}{4}$
${V_3} = 3\,Volt$
Since, ${V_3} = {V_1} - {V_Y}$
Putting values we get, ${V_Y} = {V_1} - {V_3}$
${V_Y} = 4 - 3$
$\Rightarrow {V_Y} = 1\,Volt$
So ${V_{XY}} = {V_X} - {V_Y}$
Putting values we get
${V_{XY}} = 3 - 1$
$\therefore {V_{XY}} = 2\,Volt$

Note: It should be remembered that resistance of wire is dependent on temperature. For metal or conductor resistance increases with temperature as coefficient of resistance is positive but for semiconductor resistance decreases with temperature as coefficient of resistance is negative. Conductors and semiconductors have a difference in energy gap of valence and conduction band.