Question

Find the z-score for which $ 98\% $ of the distribution’s area lies between $ - z\,{\text{and}}\,z $ .

Answer 1

Hint: We have to find the z-score for a given percentage of area in the question, for that we use the z-table to check the score on a standard normal distribution. The given percentage area is read as z-score in the table using a particular method.

Complete step-by-step answer:
We are given a percentage area of the normal distribution curve that is $ 98\% $ and we have to find its respective z-score using a z- table which is also known as standard normal table of standard normal distribution (SND).
The graph of standard normal distribution is given below

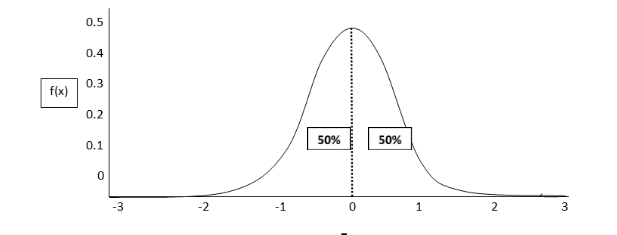
As we can see that the area under the curve is divided by the mean value of x-axis equally i.e. 50%. So we have to take 49% from mean value and see the area from -z to z.
For that we read out the following z-table in a particular way.

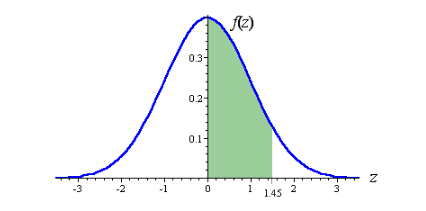
Reading z-table: We know that the mean of z-score is always zero and the z-score table indicates the percentage of values to the left of a given score on standard normal distribution. For example, if we want to see the z-score 1.45 we see the standard deviation from zero to this number on both sides of the curve like this-

Now we are supposed to check the area under this curve on both sides of the mean value using this table-

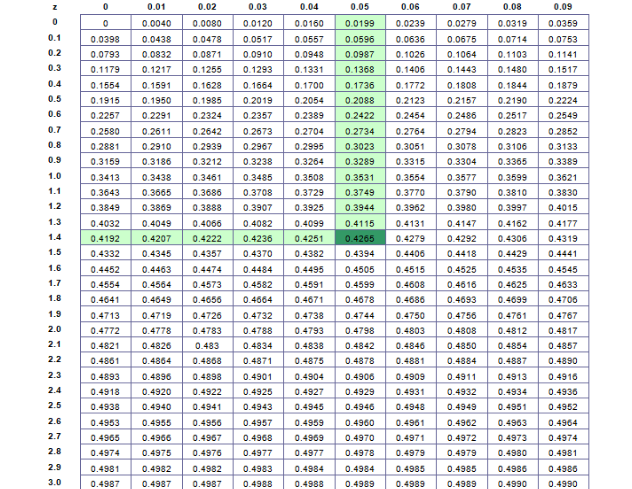
To get this area, we read down the left side of the table for the standard deviation's first 2 digits (the whole number and the first number after the decimal point, in this case 1.4), then we read across the table for the "0.05" part (the top row represents the 2nd decimal place of the standard deviation that we are interested in.)

We have: (left column) 1.4 + (top row) 0.05 = 1.45 standard deviations
So the area will be considered 42.65% on one side of the mean value and for calculating the whole area from (-z) to z we multiply it by ‘2’ i.e. $ 42.65\% \times 2 = 85.30\% $
Now applying this to our problem
We have an area of $ 98\% $ so we divide it in two parts to see what the corresponding value in the table is i.e. 49% will be read as 0.49 in the table. Now we check the value of it inside the table and reverse the process discussed in the previous example.

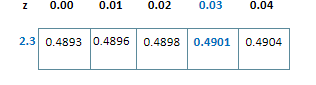
So we can see that the corresponding value: $ 2.3 + 0.03 = 2.33 $ is the z-score we get by translating the area under the curve using z-table.
So, the correct answer is “2.33”.

Note: The z-score tells you about the position of an observation in relation to the rest of the distribution which is measured in standard deviation. The data should be in normal distribution. We check the value of x-axis and then convert it into z-scores to see the actual value of observation.