Question

Find the volume of the solid obtained by revolving the loop of the curve $2a{{y}^{2}}=x{{\left( x-a \right)}^{2}}$ about the x-axis.

Answer 1

Hint: Here we have to find the volume of the solid which we will obtain after revolving the loop of the given curve $2a{{y}^{2}}=x{{\left( x-a \right)}^{2}}$. For that, we will plot the graph and we will find the range of $x$ by putting $y=0$. Then we will find the volume using integration with proper limits of $x$. The value which we will obtain after integration will be the required volume of the solid generated.

Complete step-by-step answer:
The given curve is $2a{{y}^{2}}=x{{\left( x-a \right)}^{2}}$

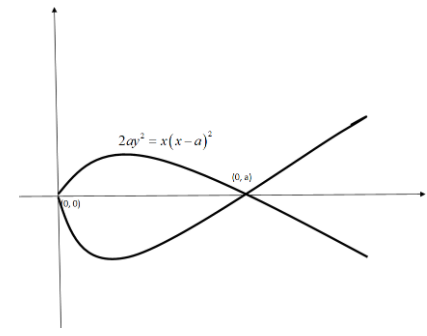
We will find the value of $x$ for which $y=0$. For that, we will put $y=0$ in the equation of the curve.
Putting value $y=0$ in the equation, we get
 $\Rightarrow 2a{{0}^{2}}=x{{\left( x-a \right)}^{2}}$
On simplifying the terms, we get
$x=0$ and $x=a$
Now, we will draw the graph of the curve.
Now, we will find the volume of solid obtained by the revolving the loop of this curve.
Therefore,
$\Rightarrow volume=\pi \int\limits_{0}^{a}{{{y}^{2}}dx}$
We will put the value of ${{y}^{2}}$here.
$\Rightarrow volume=\pi \int\limits_{0}^{a}{\dfrac{x{{\left( x-a \right)}^{2}}}{2a}dx}$
We will take constants out of integration and we will expand the terms.
$\Rightarrow volume=\dfrac{\pi }{2a}\int\limits_{0}^{a}{x\left( {{x}^{2}}+{{a}^{2}}-2ax \right)dx}$
Multiplying the terms, we get
$\Rightarrow volume=\dfrac{\pi }{2a}\int\limits_{0}^{a}{\left( {{x}^{3}}+{{a}^{2}}{{x}}-2a{{x}^{2}} \right)dx}$
Integrating the terms, we get
$\Rightarrow volume=\dfrac{\pi }{2a}\left[ \dfrac{{{x}^{4}}}{4}+\dfrac{{{a}^{2}}{{x}^{2}}}{2}-\dfrac{2a{{x}^{3}}}{3} \right]_{0}^{a}$
On further simplification, we get
$\Rightarrow volume=\dfrac{\pi }{2a}\left[ \dfrac{3{{a}^{4}}+6{{a}^{4}}-8{{a}^{4}}}{12} \right]$
 $\Rightarrow volume=\dfrac{\pi {{a}^{3}}}{24}$
Hence, the required volume of the solid obtained by revolving the loop of this curve is $\dfrac{\pi {{a}^{3}}}{24}$ cubic units.

Note: This curve is symmetric about the x-axis. A curve is said to be symmetric about the x axis if whenever a point $\left( a,b \right)$ lies on the curve then point $\left( a,-b \right)$ also lies on the curve i.e. both of them will satisfy the equation of the curve. Here x-axis is called the axis of symmetry of the given curve. The shape of the curve is the same on both sides of the axis of symmetry.