
Find the volume of the rectangular tank whose length, breadth, and depth (in units) are
(a) \[\dfrac{4}{9}xy,\dfrac{2}{15}x{{y}^{3}},\dfrac{75}{16}{{x}^{3}}z\]
(b) \[\left( x-y \right),\left( x+y \right),\left( {{x}^{2}}-{{y}^{2}} \right)\]
Answer
558k+ views
Hint: In part (a), the length, breadth, and height of a rectangular tank are given. The formula for the volume, Volume = Length \[\times \] Breadth \[\times \] Height. Now, use the length, breadth, and height to calculate the volume of the tank. Similarly, calculate the volume of the tank in part (b) as well.
Complete step-by-step answer:
According to the question, we are given the length, breadth, and height of a rectangular tank.
We know that a rectangular tank is of cuboidal shape.
Here, in this question, we are asked to find the volume of the rectangular tank.
We know that the volume of the cuboid is the product of its length, breadth, and height, that is, Volume of a cuboid = Length \[\times \] Breadth \[\times \] Height ……………………………………..(1)
Since the rectangular tank is of cuboidal shape so, the formula for the volume of cuboid will be applicable for the volume of the rectangular tank too ……………………………………….(2)
From equation (1) and equation (2), we have
The volume of the rectangular tank = Length \[\times \] Breadth \[\times \] Height …………………………………….(3)
(a) We are given that,
The length of the tank = \[\dfrac{4}{9}xy\] units ………………………………………………(4)
The breadth of the tank = \[\dfrac{2}{15}x{{y}^{3}}\] units ………………………………………(5)
The depth of the tank = The height of the tank = \[\dfrac{75}{16}{{x}^{3}}z\] units …………………………………………..(6)
Now, from equation (3), equation (4), equation (5), and equation (6), we get
The volume of the rectangular tank = \[\dfrac{4}{9}xy\times \dfrac{2}{15}x{{y}^{3}}\times \dfrac{75}{16}{{x}^{3}}z=\dfrac{5}{18}{{x}^{5}}{{y}^{4}}z\] .
Therefore, the volume of the rectangular tank is \[\dfrac{5}{18}{{x}^{5}}{{y}^{4}}z\] .
(b) Similarly, we are given that,
The length of the tank = \[\left( x-y \right)\] units ………………………………………………(7)
The breadth of the tank = \[\left( x+y \right)\] units ………………………………………(8)
The depth of the tank = The height of the tank = \[\left( {{x}^{2}}-{{y}^{2}} \right)\] units …………………………………………..(9)
Now, from equation (3), equation (7), equation (8), and equation (9), we get
The volume of the rectangular tank = \[\left( x-y \right)\times \left( x+y \right)\times \left( {{x}^{2}}-{{y}^{2}} \right)\] \[=\left( {{x}^{2}}-{{y}^{2}} \right)\left( {{x}^{2}}-{{y}^{2}} \right)={{x}^{4}}+{{y}^{4}}-2{{x}^{2}}{{y}^{2}}\] .
Therefore, the volume of the rectangular tank is \[\left( {{x}^{4}}+{{y}^{4}}-2{{x}^{2}}{{y}^{2}} \right)\] .
Note: Here, one might question how a rectangular tank is of cuboidal shape. Since a base of rectangular shape has some length as well as the breadth and if the rectangular base is given some height then, we can observe that a cuboid is formed.
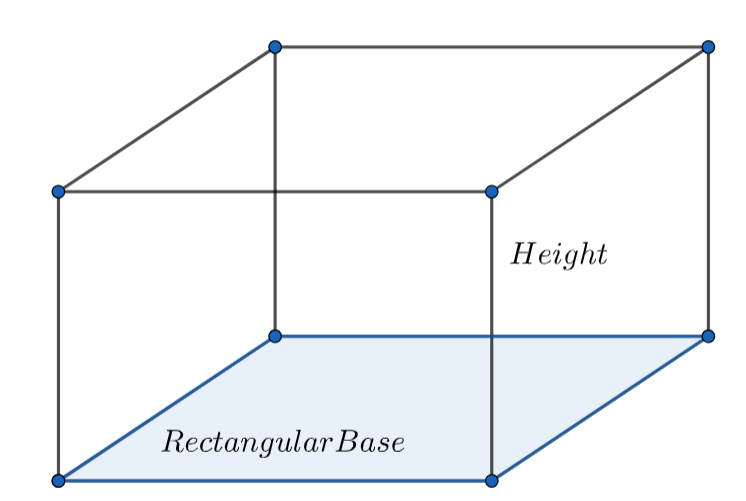
Complete step-by-step answer:
According to the question, we are given the length, breadth, and height of a rectangular tank.
We know that a rectangular tank is of cuboidal shape.
Here, in this question, we are asked to find the volume of the rectangular tank.
We know that the volume of the cuboid is the product of its length, breadth, and height, that is, Volume of a cuboid = Length \[\times \] Breadth \[\times \] Height ……………………………………..(1)
Since the rectangular tank is of cuboidal shape so, the formula for the volume of cuboid will be applicable for the volume of the rectangular tank too ……………………………………….(2)
From equation (1) and equation (2), we have
The volume of the rectangular tank = Length \[\times \] Breadth \[\times \] Height …………………………………….(3)
(a) We are given that,
The length of the tank = \[\dfrac{4}{9}xy\] units ………………………………………………(4)
The breadth of the tank = \[\dfrac{2}{15}x{{y}^{3}}\] units ………………………………………(5)
The depth of the tank = The height of the tank = \[\dfrac{75}{16}{{x}^{3}}z\] units …………………………………………..(6)
Now, from equation (3), equation (4), equation (5), and equation (6), we get
The volume of the rectangular tank = \[\dfrac{4}{9}xy\times \dfrac{2}{15}x{{y}^{3}}\times \dfrac{75}{16}{{x}^{3}}z=\dfrac{5}{18}{{x}^{5}}{{y}^{4}}z\] .
Therefore, the volume of the rectangular tank is \[\dfrac{5}{18}{{x}^{5}}{{y}^{4}}z\] .
(b) Similarly, we are given that,
The length of the tank = \[\left( x-y \right)\] units ………………………………………………(7)
The breadth of the tank = \[\left( x+y \right)\] units ………………………………………(8)
The depth of the tank = The height of the tank = \[\left( {{x}^{2}}-{{y}^{2}} \right)\] units …………………………………………..(9)
Now, from equation (3), equation (7), equation (8), and equation (9), we get
The volume of the rectangular tank = \[\left( x-y \right)\times \left( x+y \right)\times \left( {{x}^{2}}-{{y}^{2}} \right)\] \[=\left( {{x}^{2}}-{{y}^{2}} \right)\left( {{x}^{2}}-{{y}^{2}} \right)={{x}^{4}}+{{y}^{4}}-2{{x}^{2}}{{y}^{2}}\] .
Therefore, the volume of the rectangular tank is \[\left( {{x}^{4}}+{{y}^{4}}-2{{x}^{2}}{{y}^{2}} \right)\] .
Note: Here, one might question how a rectangular tank is of cuboidal shape. Since a base of rectangular shape has some length as well as the breadth and if the rectangular base is given some height then, we can observe that a cuboid is formed.

Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is pollution? How many types of pollution? Define it

What is the Full Form of ISI and RAW




