Question

Find the volume of the parallelepiped whose co terminal edges are \[4\hat{i}+3\hat{j}+\hat{k},5\hat{i}+9\hat{j}+19\hat{k}\text{ }and\text{ }8\hat{i}+6\hat{j}+5\hat{k}\].

Answer 1

Hint: The volume of the parallelepiped is given by, $\vec{a}.\left( \vec{b}\times \vec{c} \right)$ where $\vec{a},\vec{b},\vec{c}$ are the coterminal edges of the parallelepiped. We have already been given the co terminal edges, so we will put $\vec{a}=4\hat{i}+3\hat{j}+\hat{k},\vec{b}=5\hat{i}+9\hat{j}+19\hat{k},\vec{c}=8\hat{i}+6\hat{j}+5\hat{k}$ and find the volume of the parallelepiped.

Complete step-by-step answer:
It is given in the question that we have to find the volume of the parallelepiped whose co terminal edges are \[4\hat{i}+3\hat{j}+\hat{k},5\hat{i}+9\hat{j}+19\hat{k}\text{ }and\text{ }8\hat{i}+6\hat{j}+5\hat{k}\]. So, before we solve the question, let us understand what a parallelepiped is. It is a solid 3D shape in which all the faces are parallelograms and the opposite faces are of the same dimension. A parallelepiped can be shown as below.

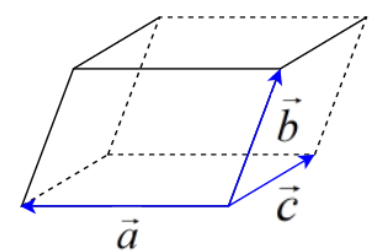
Let us assume that $\vec{a}=4\hat{i}+3\hat{j}+\hat{k},\vec{b}=5\hat{i}+9\hat{j}+19\hat{k},\vec{c}=8\hat{i}+6\hat{j}+5\hat{k}$. Then, we know that the volume of a parallelepiped is given by, $\vec{a}.\left( \vec{b}\times \vec{c} \right)$ where $\vec{a},\vec{b},\vec{c}$ are the coterminal edges of the parallelepiped.
So, first, we will find the cross product of $\vec{b}\text{ }and\text{ }\vec{c}$. In order to find the cross product, we will take determinant of the given vectors. For example, let $\vec{p}=a\hat{i}+b\hat{j}+c\hat{k}\text{ }and\text{ }\vec{q}=d\hat{i}+e\hat{j}+f\hat{k}$, then their cross product will be, $\vec{p}\times \vec{q}=\left| \begin{matrix}
   {\hat{i}} & {\hat{j}} & {\hat{k}} \\
   a & b & c \\
   d & e & f \\
\end{matrix} \right|$.
And, the determinant will be, $\hat{i}\left( bf-ec \right)-\hat{j}\left( af-dc \right)+\hat{k}\left( ae-db \right)$.
So, here, we have to find the cross product of $\vec{b}\text{ }and\text{ }\vec{c}$, where $\vec{b}=5\hat{i}+9\hat{j}+19\hat{k},\vec{c}=8\hat{i}+6\hat{j}+5\hat{k}$. So, we will get,
$\vec{b}\times \vec{c}=\left| \begin{matrix}
   {\hat{i}} & {\hat{j}} & {\hat{k}} \\
   5 & 9 & 19 \\
   8 & 6 & 5 \\
\end{matrix} \right|$
So, on taking the determinant, we get,
\[\begin{align}
  & \hat{i}\left[ \left( 9\times 5 \right)-\left( 6\times 19 \right) \right]-\hat{j}\left[ \left( 5\times 5 \right)-\left( 8\times 19 \right) \right]+\hat{k}\left[ \left( 5\times 6 \right)-\left( 8\times 9 \right) \right] \\
 & \hat{i}\left[ 45-114 \right]-\hat{j}\left[ 25-152 \right]+\hat{k}\left[ 30-72 \right] \\
 & -69\hat{i}+127\hat{j}-42\hat{k} \\
\end{align}\]
So, we get the cross product of $\vec{b}\text{ }and\text{ }\vec{c}$ as \[-69\hat{i}+127\hat{j}-42\hat{k}\].
Now, we will find the dot product of $\vec{a}$ with $\vec{b}\times \vec{c}$.
If we consider the vectors, $\vec{p}=a\hat{i}+b\hat{j}+c\hat{k}\text{ }and\text{ }\vec{q}=d\hat{i}+e\hat{j}+f\hat{k}$, then their dot product will be $\vec{p}.\vec{q}=\left( a\times d \right)+\left( b\times e \right)+\left( c\times f \right)$.
So, here we have to find the dot product of $\vec{a}$ with $\vec{b}\times \vec{c}$, where $\vec{a}=4\hat{i}+3\hat{j}+\hat{k}$ and \[\vec{b}\times \vec{c}=-69\hat{i}+127\hat{j}-42\hat{k}\]. So, we will get,
\[\begin{align}
  & \vec{a}.\left( \vec{b}\times \vec{c} \right)=\left( 4\hat{i}+3\hat{j}+\hat{k} \right)\left( -69\hat{i}+127\hat{j}-42\hat{k} \right) \\
 & =\left( 4\times -69 \right)+\left( 3\times 127 \right)+\left( 1\times -42 \right) \\
 & =-276+381-42 \\
 & =381-18 \\
 & =63\text{ }cubic\text{ }units \\
\end{align}\]
Therefore, the volume of the parallelepiped is 63 cubic units.

Note: The most common mistake that students make while solving this question is that, while taking the determinant, most of the students put + sign instead of – sign before $\hat{j}$ and as a result, they will get the cross product of $\vec{b}\text{ }and\text{ }\vec{c}$ as \[\vec{b}\times \vec{c}=-69\hat{i}-127\hat{j}-42\hat{k}\], which is wrong, hence the final answer also will become wrong. So, the students are supposed to do all the calculations step by step in order to avoid any mistakes.