Question

How do you find the volume of a Hershey’s kiss using the “disk method”?

Answer 1

Hint: In this question we have to find the volume of a Hershey’s kiss which is a chocolate manufactured by the Hershey’s company. It is in the shape of a cone but it is non uniform therefore the volume cannot be found out directly by using the volume of a cone formula. The disk method is a method to find the volume by cutting out a finite number of disks. We then find the area of all the circles which are the disks from height to height and all of them to get the required volume.

Complete step by step solution:
Consider the height of Hershey's kiss to be $h$. And since we are finding the area of a circle the function will be as:
$\Rightarrow \pi \times {{\left( r\left( h \right) \right)}^{2}}$, where the function $r\left( h \right)$ denotes the radius of the Hershey’s kiss at height $h$.
Now since we have to add all the areas to get the volume of the Hershey’s kiss, we will integrate it therefore, we can write it as:
$\Rightarrow \int{\pi \times {{\left( r\left( h \right) \right)}^{2}}}$
Now to calculate the exact volume we need the value of the profile function which is $r\left( h \right)$. Now since we do not know the exact profile function, we will use a profile function which is very close to it, which is $\cos \left( h \right)$. The graph of $\cos \left( h \right)$ is like:

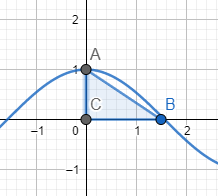
It can be seen that figure $\text{ABC}$ closely models the shape of the cross section of a Hershey’s kiss in two dimensions.
Therefore, on substituting, we get:
$\Rightarrow \int{\pi \times {{\left( \cos \left( h \right) \right)}^{2}}}$
Now if the height $h$ is known, then the function can be integrated from $0$ to $h$, to get the estimated volume. The function becomes:
$\Rightarrow \int_{0}^{h}{\pi \times {{\left( \cos \left( h \right) \right)}^{2}}}dy$, which is the required answer.

Note: It is to be remembered that this is just an approximate answer to the volume. To get the actual volume we need the equation of the curve for Hershey's kiss.
Another profile function which can be used is $y=\sqrt{h}$ which has a graph as:

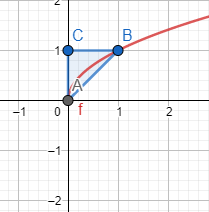
It can be seen that the figure $\text{ABC}$ is in the shape of a cross section of a Hershey’s kiss.
Now the main function is:
$\Rightarrow \pi \times {{\left( r\left( h \right) \right)}^{2}}$
Now since we have to put the value of $h$ but it is in square root, we will square the equation as ${{y}^{2}}=h$ and substitute the value of $h$. On substituting, we get:
$\Rightarrow \pi \times {{\left( {{y}^{2}} \right)}^{2}}$
Which can be simplified as:
$\Rightarrow \pi \times {{y}^{4}}$
Therefore, the integration will be $\int_{0}^{h}{\pi \times {{y}^{4}}}dy$, which is another solution.