Question

How do you find the volume of a \[3D\] trapezoid?

Answer 1

Hint: In order to determine the volume of trapezoid. First, we need to draw a diagram for the trapezoid having the area and length. The formula can be used to calculate the area of a trapezoid, \[A = \dfrac{1}{2}h(a + b)\] .Where, h is the height and \[a\] and \[b\] are the lengths of the parallel sides. Volume of \[3D\] trapezoid calculated by the four variable formula, \[\;V = {\text{ }}\dfrac{1}{2}L(a + b)h\] . Where, the length be \[L\] and the area is denoted as \[A\] .

Complete step by step solution:
In this problem,
We have to find the volume of a \[3D\] trapezoid
We need to find the area of the base of the trapezium to calculate the volume.
We need to find the area of the trapezoid can be simply defined as the average length of the sides multiplied by the height, using the variables to draw a diagram for representing the area of trapezoid,

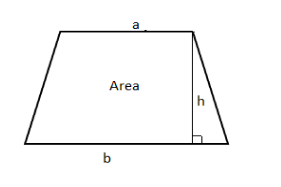
This is the formula for the area of trapezium, \[A = \dfrac{1}{2}h(a + b)\]
Let \[A\] be the trapezoidal Area
Let \[h\] be the Trapezoidal height.
Let \[a\] be the top width and \[b\] be the top width.
The volume does not exist in two-dimensional statistics. So, you could construct a trapezoidal trapezoid, which is a three-dimensional figure with a trapezoid base. To determine the volume of something, you must first determine the area.
 To translate this concept into the three dimension diagram, simply multiply by the trapezoid length:
If the trapezoid length is \[L\] , trapezoid base width \[b\] , trapezoid top width \[a\] , and trapezoid height \[h\] . We can draw a three dimensional figure as follows.

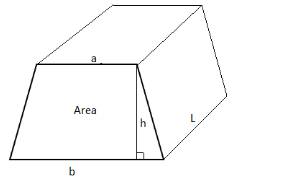
The volume of a \[3D\] trapezoid is calculated using the four-variable formula,
 \[\;V = \dfrac{1}{2}L \times h(a + b)\] .
Where,
  \[V\] Trapezoidal Volume
 \[h\] is the Trapezoidal height.
 \[a\] The top's length
 \[b\] The bottom's length
 \[L\] is the trapezoid's height.
Finally, we use these methods to find the volume of trapezoid for any given values.
So, the correct answer is “ \[\;V = \dfrac{1}{2}L \times h(a + b)\] ”.

Note: For example, If the trapezoid length is \[8cm\] , trapezoid base width \[6.5cm\] , trapezoid top width \[1.5cm\] , and trapezoid height \[4.2cm\] .
We can draw a three dimensional figure with respect to the values given as follows.

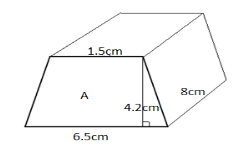
 To find the area of trapezoid from the formula, we get
 \[A = \dfrac{1}{2}h(a + b)\]
By substitute the values into the formula, we can get
 \[A = \dfrac{1}{2} \times 4.2(1.5 + 6.5) = 16.8c{m^2}\]
Now, we have to calculate the three dimensional volume of trapezoid is multiplied with length and area of trapezoid, we have
 \[\;V = {\text{ }}\dfrac{1}{2}L(a + b)h = 16.8c{m^2} \times 8cm\]
Since, the area is already calculated. So we put that value and the length is given in the figure.
Therefore, the volume of a three dimensional trapezoid is simplified as \[\;V = {\text{ 134c}}{{\text{m}}^3}\] .