Question

How do you find the volume bounded by \[x = 8 - {y^2}\] and \[x = {y^2}\] revolved about the \[y - axis\] ?

Answer 1

Hint: To find the volume bounded by \[x = 8 - {y^2}\] and \[x = {y^2}\] on the \[y - axis\] . To plot a graph with respect to given equations. By using Pappu’s second theorem, the volume, \[V\] of a solid of revolution generated by the revolution of a lamina about an external axis is equal to the product of the area \[A\] of the lamina and the distance travelled by the lamina’s geometric centroid,
 \[V = A \times \] Distance
The centroid will travel a distance of \[2\pi x\]

Complete step-by-step answer:
The volume bounded region by the given equations are revolved around \[y - axis\] ,
 \[x = 8 - {y^2}\] ……… \[(1)\]
 \[x = {y^2}\] …….. \[(2)\]
We need the point where the two parabolas equations are intersect \[8 - {y^2}\] and \[{y^2}\] , we get
 \[8 - {y^2} = {y^2}\]
To simplify it,
 \[
  {y^2} + {y^2} = 8 \\
  2{y^2} = 8 \;
 \]
Now, we get
 \[
  {y^2} = \dfrac{8}{2} = 4 \\
  {y^2} = {2^2} \;
 \]
By taking square root on both sides, we get
Therefore,
 \[y = \pm 2\] , by substitute the value in equation \[(2)\] to find \[x\] , we have
 \[(2) \Rightarrow x = {2^2} = 4\]
Here, we have the point \[(x,y)\] is \[(4, \pm 2)\] \[\]
By the two parabolas and the points \[(4, - 2),(4,2)\] , we have to plot a graph is mentioned below

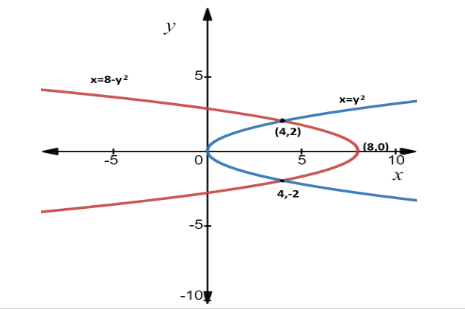
By using Pappus second theorem,
The volume \[V\] of a solid of revolution generated by the revolution of a lamina about an external axis is equal to the product of the area \[A\] of the lamina and the distance travelled by the lamina’s geometric centroid.
 \[V = A \times \] Distance
For one revolution about the \[y\] -axis,
Due to symmetric, the geometric centroid is at the point \[(4,0)\]
The centroid will travel a distance of \[2\pi x = 2\pi \cdot 4\]
Distance \[ = 8\pi \]
The total area \[A\] is the four times of the area of one revolution (which is quarter of the area) about \[y - axis\] .
The curve represents \[x = {y^2}\] which implies \[y = \sqrt x \]
Total area, \[A = 4\int\limits_0^4 {ydx} \]
By substitute the value \[y\] ,
 \[A = 4\int\limits_0^4 {\sqrt x dx} \]
By integrating the above with respect to \[x\] , we get
 \[ = 4\left[ {\dfrac{{{x^{\dfrac{1}{2} + 1}}}}{{\dfrac{1}{2} + 1}}} \right] _0^4\]
To simplify, we get
 \[ = 4\left[ {\dfrac{{{x^{\dfrac{1}{2}}} \cdot {x^1}}}{{\dfrac{3}{2}}}} \right] _0^4\]
Now, we get
 \[ = 4 \cdot \dfrac{2}{3}\left[ {x \cdot {x^{\dfrac{1}{2}}}} \right] _0^4\]
By applying upper limit and lower limit for \[x\] , we get
 \[ = 4 \cdot \dfrac{2}{3}\left[ {4 \cdot {4^{\dfrac{1}{2}}}} \right] \]
By simplify the multiplication, then we get
 \[ = \dfrac{8}{3}\left[ 8 \right] \]
Total area, \[A\] \[ = \dfrac{{64}}{3}\]
Hence, the volume \[V = A \times \] distance
 \[V = \dfrac{{64}}{3} \times 8\pi \]
So, the correct answer is “ \[V = \dfrac{{64}}{3} \times 8\pi \] ”.

Note: We need to find the volume bounded with the points found from the two parabola equations, we should remind the volume formula to solve the problem and to find the total area by means of the formula.