Question

How do you find the vertex of a quadratic equation?

Answer 1

Hint:
Quadratic equation is also called a parabola. The vertex of a quadratic equation of parabola is nothing but the highest or the lowest point of the quadratic equation. In order to find the vertex of the quadratic equation which is represented as $a{x^2} + bx + c = y$ which is the standard form. And the vertex can be found by using the formula $\dfrac{{ - b}}{{2a}}$ for the $x$ coordinate.

Complete Step by Step Solution:
Quadratic equation is also called as parabola which can be represented in the form of an equation as $a{x^2} + bx + c = y$
Where $x$ and $y$ are coordinates of $x$ and $y$ axis respectively
$a,b,c$ are constants.
Vertex of the quadratic equation is nothing but the highest or the lowest point of the quadratic equation. Which is as shown in the below diagram.

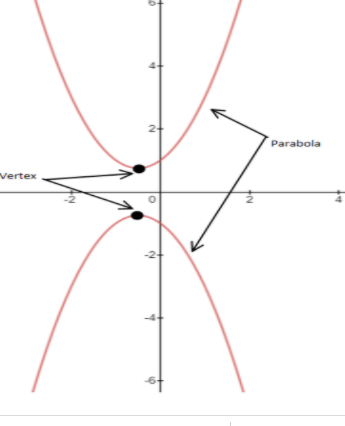
The above diagram shows a rough sketch of a parabola and the vertex is as shown.
There are some steps to be followed to find the vertex of a quadratic equation.
Step 1: First step is to have a quadratic equation in the form of $a{x^2} + bx + c = y$ .
Step 2: Now, try to calculate the vertex by using the formula $\dfrac{{ - b}}{{2a}}$ for x coordinate.
Step 3: Now to calculate y coordinate, substitute the value of x you got from the step 2 in the given equation, and solve for y coordinate.

Note:
In the quadratic equation you get only one vertex that is a higher vertex or the lower vertex of a parabola. Only if they give complex problems then you get both in the same graph. While finding out the vertex of the quadratic equation be careful while taking the constant terms.