Question

How do you find the vertex and the intercepts for $y=3{{x}^{2}}+12x$?

Answer 1

Hint: The equation $y=3{{x}^{2}}+12x$ is linear in $y$ but quadratic in $x$. So this means that this is an equation of a parabola. For determining the x-intercept, we will put $y=0$ in the given equation. And for determining the y-intercept, we will put $x=0$. But for the determination of the vertex, we will differentiate the given equation and equate the derivative to zero. This is because at the vertex of a parabola, its slope is equal to zero.

Complete step by step solution:
The given equation is
$y=3{{x}^{2}}+12x........\left( i \right)$
We know that the x-intercepts are the points where the graph cuts the x-axis. Therefore, we put $y=0$ in (i) to get
\[\begin{align}
  & \Rightarrow 0=3{{x}^{2}}+12x \\
 & \Rightarrow 3{{x}^{2}}+12x=0 \\
\end{align}\]
Taking $x$ common we have
$\begin{align}
  & \Rightarrow x\left( 3x+12 \right)=0 \\
 & \Rightarrow x=0,x=\dfrac{-12}{3} \\
 & \Rightarrow x=0,x=-4 \\
\end{align}$
Therefore, the x-intercepts are $\left( 0,0 \right)$ and $\left( -4,0 \right)$.
Now, the y-intercepts are the points where the graph cuts the y-axis. Therefore, we put $x=0$ in (i) to get
$\begin{align}
  & \Rightarrow y=3{{\left( 0 \right)}^{2}}+12\left( 0 \right) \\
 & \Rightarrow y=0 \\
\end{align}$
So the y-intercept is $\left( 0,0 \right)$.
Now, since the given equation is quadratic in $x$ and linear in $y$, this means that it is an equation of a parabola whose axis is vertical. We know that at the vertex of a parabola having a vertical axis, its slope is equal to zero. Therefore, we differentiate both sides of the given equation (i) to get
$\begin{align}
  & \Rightarrow \dfrac{dy}{dx}=3\left( 2x \right)+12 \\
 & \Rightarrow \dfrac{dy}{dx}=6x+12 \\
\end{align}$
For vertex, we put $\dfrac{dy}{dx}=0$ to get
$\begin{align}
  & \Rightarrow 6x+12=0 \\
 & \Rightarrow x=-\dfrac{12}{6} \\
 & \Rightarrow x=-2 \\
\end{align}$
So the x-coordinate of the vertex is equal to $-2$. For the y-coordinate, we substitute $x=-2$ in (i) to get
$\begin{align}
  & \Rightarrow y=3{{\left( -2 \right)}^{2}}+12\left( -2 \right) \\
 & \Rightarrow y=3\left( 4 \right)-24 \\
 & \Rightarrow y=12-24 \\
 & \Rightarrow y=-12 \\
\end{align}$
So the y-coordinate of the vertex is equal to $-12$. Therefore, the vertex of the given equation is at $\left( -2,-12 \right)$.
We can observe the vertex and the intercepts in the below graph.

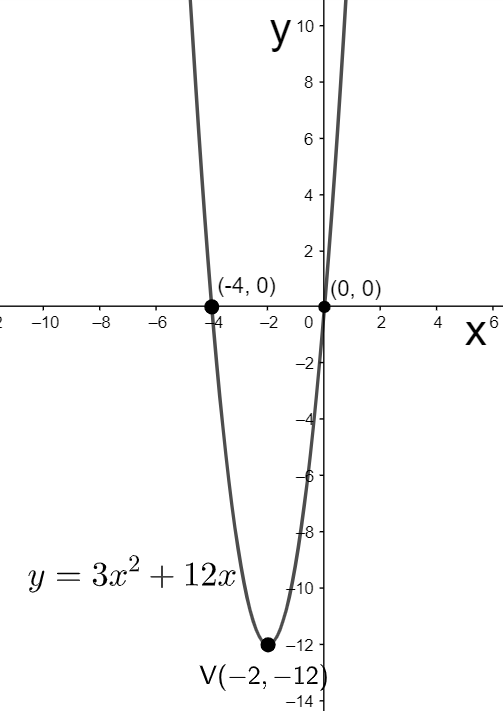
Note:
For determining the vertex, we can also use the completing the square method so that the given equation gets reduced to the standard equation of a parabola. The standard equation of a parabola is given as ${{X}^{2}}=4aY$, from which the vertex is at $X=0,Y=0$. By completing the square method, we will obtain the given equation as $\left( x+2 \right)=\dfrac{1}{3}\left( y+12 \right)$. Therefore, setting $x+2=0$ and $y+12=0$ we will get the vertex at $\left( -2,-12 \right)$.