Question

Find the values of ‘a’ and ‘b’ of the parallelogram PQRS. Given that: vertices of the parallelogram PQRS contains$P \equiv (1,2)$, $Q \equiv (4,6)$,$R \equiv (5,7)$and $S \equiv (a,b)$ respectively.
(a) $a = 3$,$b = 3$
(b) $a = 3$,$b = 2$
(c) Cannot be determined
(d) $a = 2$,$b = 3$

Answer 1

Hint: We will use the most eccentric concept of vectors. Consider the midpoint of the polygon, say, parallelogram between the diagonals which intersect at one point. Then, using the midpoint formula, substituting the given vertices in the formula, the required values are obtained.

Complete step-by-step answer:
Since, we have given that
The parallelogram PQRS has the vertices ‘P’ , ‘Q’ , ‘R’ and ‘S’ respectively
Vertices are as follows,
$P = (1,2)$,
$Q = (4,6)$,
$R = (5,7)$ and
$S = (a,b)$

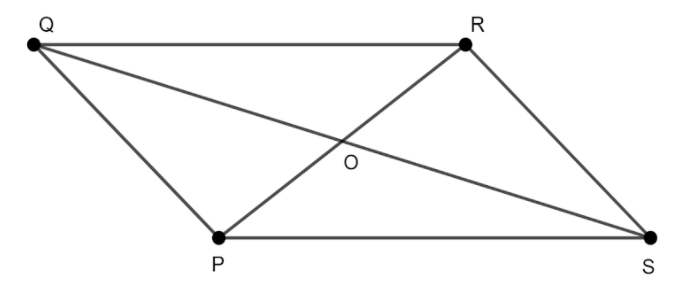
From figure, it seems that
Diagonals ‘PR’ and ‘QS’ meets at one point ‘O’ intersects at only and only one point respectively,
As a result by midpoint formula that is $x = \dfrac{{a + b}}{2}$ and $y = \dfrac{{c + d}}{2}$, we get
Hence, here we can write
\[\dfrac{{\overrightarrow {PR} }}{2} = \dfrac{{\overrightarrow {QS} }}{2}\]
Using midpoint formula, we get
Since, considering x-intercept
\[\dfrac{{\overrightarrow p + \overrightarrow r }}{2} = \dfrac{{\overrightarrow q + \overrightarrow s }}{2}\]
Substituting the given vertices in above equation, we get
\[
  \dfrac{{1 + 5}}{2} = \dfrac{{4 + a}}{2} \\
  \dfrac{6}{2} = \dfrac{{4 + a}}{2} = 3 \\
\]
Solve the equation mathematically, we get
\[
  6 = 4 + a \\
  \therefore a = 6 - 4 = 2 \\
\]
Similarly,
Using midpoint formula, we get
Since, considering y-intercept
\[\dfrac{{\overrightarrow p + \overrightarrow r }}{2} = \dfrac{{\overrightarrow q + \overrightarrow s }}{2}\]
Substituting the given vertices in above equation, we get
\[
  \dfrac{{2 + 7}}{2} = \dfrac{{6 + b}}{2} \\
  \dfrac{9}{2} = \dfrac{{6 + b}}{2} \\
\]
Solve the equation mathematically, we get
\[
  9 = 6 + b \\
  \therefore b = 9 - 6 = 3 \\
\]
So, the correct answer is “Option d”.

Note: One must remember the concept of vector quantity that revolves in magnitude as well as direction of the quantities or applications of the respective parameters. Should clarify how to calculate the required values of the vertices of the required polygon – using the midpoint formula (after joining diagonals of the polygon, say, parallelogram). Algebraic identities play a significant role in solving this problem so as for the ease of such problems.