Question

Find the value of x and y in the following figure

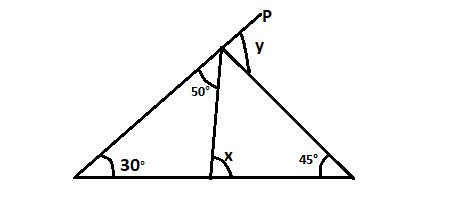
Answer 1

Hint: We will first use the property of the triangle i.e. the sum of all interior angles and property of straight line i.e. linear pair to find the angles of the triangle, and will get the value of x.
Now using the property of the exterior angle of the triangle we will find the measures of y.

Complete step-by-step answer:

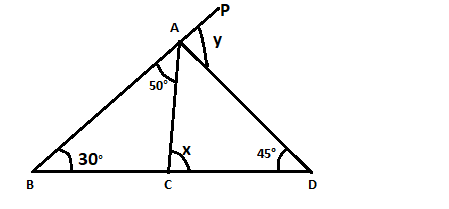
 $\angle ABC = {30^ \circ }$
 $\angle BAC = {50^ \circ }$
 $\angle D = {45^ \circ }$
Now we know that sum all angles of a triangle measures ${180^ \circ }$
Therefore, in triangle ABC, we can say that
 $ \Rightarrow \angle ABC + \angle BAC + \angle ACB = {180^ \circ }$
Now substituting the values of angles $\angle ABC$ and $\angle BAC$, we get,
 $ \Rightarrow {30^ \circ } + {50^ \circ } + \angle ACB = {180^ \circ }$
Subtracting ${80^ \circ }$ from both the sides, we get,
 $\therefore \angle ACB = {100^ \circ }$
We know that in a straight line the sum of angles is ${180^ \circ }$ and it is known as a linear pair.
As we can see that BCD is a straight line then using linear pair we can say that
 $ \Rightarrow \angle ACB + x = {180^ \circ }$
Substituting the value of $\angle ACB$
 $ \Rightarrow {100^ \circ } + x = {180^ \circ }$
Subtracting ${100^ \circ }$ from both the sides
 $ \Rightarrow x = {80^ \circ }$
We know that the measure of an exterior angle of a triangle is equal to the sum of the interior opposite two angles of the triangle.
Now using this property, we can say that
In triangle ABD, we have,
 $ \Rightarrow y = \angle B + \angle D$
Substituting the value of $\angle B$ and $\angle D$ , we get,
 $ \Rightarrow y = {30^ \circ } + {45^ \circ }$
On simplification we get,
 $ \Rightarrow y = {75^ \circ }$
Therefore the measures of the angles x and y are ${80^ \circ }$ and ${75^ \circ }$ respectively.
Note: Places where at a single point multiple angles are forming like at point A, we should always properly name the triangle like if we use $\angle A$ in place of $\angle BAC$, it will not be cleared of which angle we are talking about as y is also forming at the point A, so remember to properly name these types of angles.