Question

: Find the value of x + y + z in figure 1 and x + y + z + w in figure 2.

Answer 1

Hint: Use the property sum of an exterior angle, and the corresponding interior angle of a polygon is $180{}^\circ $ . Also, use the property that the sum of all the interior angles of an n-sided polygon is $\left( n-2 \right)180{}^\circ $.

Complete step by step answer:
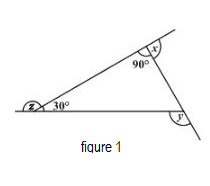
Let us first start with figure 1.

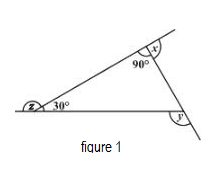
Figure 1 is a Rights angled triangle. Now, using the property that sum of an exterior angle and the corresponding interior angle of a polygon is $180{}^\circ $ , we get
$\begin{align}
  & z+30{}^\circ =180{}^\circ \\
 & \Rightarrow z=150{}^\circ \\
\end{align}$
$\begin{align}
  & x+90{}^\circ =180{}^\circ \\
 & \Rightarrow x=90{}^\circ \\
\end{align}$
Now according to the exterior angle property of the triangle, the exterior angle of a triangle is the sum of the opposite interior angles.
$\therefore y=90{}^\circ +30{}^\circ =120{}^\circ $
Therefore, x + y + z = $360{}^\circ $ for figure 1.
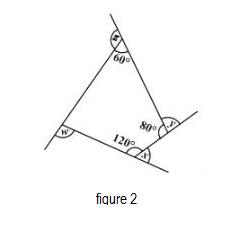
Now let us move to figure 2.
 

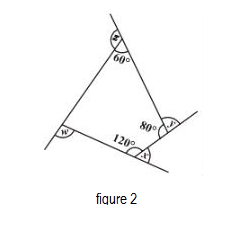
Figure 2 is a quadrilateral. Let the unknown interior angle of the quadrilateral be p.
Now, using the property that sum of an exterior angle and the corresponding interior angle of a polygon is $180{}^\circ $ , we get:
$\begin{align}
  & z+60{}^\circ =180{}^\circ \\
 & \Rightarrow z=120{}^\circ \\
\end{align}$
$\begin{align}
  & x+120{}^\circ =180{}^\circ \\
 & \Rightarrow x=60{}^\circ \\
\end{align}$
$\begin{align}
  & y+80{}^\circ =180{}^\circ \\
 & \Rightarrow y=100{}^\circ \\
\end{align}$
We know that the sum of all the interior angles of a quadrilateral is equal to $360{}^\circ .$ Therefore, the unknown angle of the quadrilateral comes out to be:
$\begin{align}
  & p+60{}^\circ +80{}^\circ +120{}^\circ =360{}^\circ \\
 & \Rightarrow p=100{}^\circ \\
\end{align}$
And using the property that sum of an exterior angle and the corresponding interior angle of a polygon is $180{}^\circ $ , we get
$\begin{align}
  & p+w=180{}^\circ \\
 & 100{}^\circ +w=180{}^\circ \\
 & w=80{}^\circ \\
\end{align}$
Therefore, we can conclude that x + y + z + w = $360{}^\circ $ in case of figure 2.

Note: The above question is based on the theorem that the sum of all the exterior angles of a polygon are $360{}^\circ $ . However, while solving such questions, it is a good practice to ensure that you are using all the data provided in the question.