
Find the value of $\sqrt{2401}$ using the prime factorization method.
Answer
624.3k+ views
Hint:Firstly get the prime factors of the given number as we do in LCM and HCF and then equate the number with the multiplication of factors. Arrange the same factors in pairs and then take square root on the both sides to get the final answer.
Complete step by step answer:
We will write down the given number first, therefore,
$\sqrt{2401}$
In prime factorization method we have to get the prime factors of the given number and for that we will divide the given number by the lowest number by which it is completely,
As 2401 is completely divisible by the number 7 therefore we get,
$\dfrac{2401}{7}=343$
Therefore 7 is first prime factor of 2401 now we will do the same thing with 343 therefore,
\[\dfrac{343}{7}=49\]
Therefore the second prime factor is also 7, likewise we will proceed and get,
$\dfrac{49}{7}=7$
Therefore,
\[\dfrac{7}{7}=1\]
As the remainder is 1 therefore we can say that we have done with all the prime factors and we have listed below in simplest manner,
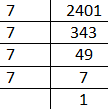
Now as we know that the prime factor listed above if multiplies constitutes the given number 2401 therefore we can write,
$\therefore 7\times 7\times 7\times 7=2401$
If we use the formula ${{a}^{m}}{{a}^{n}}={{a}^{m+n}}$ we will get,
$\therefore {{7}^{2}}\times {{7}^{2}}=2401$
As we have to find the square root of the given number therefore taking square roots on the both sides of the equation we will get,
$\therefore \sqrt{{{7}^{2}}\times {{7}^{2}}}=\sqrt{2401}$
If we cancel the square and the square root from the left hand side of the equation we will get,
$\therefore 7\times 7=\sqrt{2401}$
By multiplying and rearranging the above equation we will get,
$\therefore \sqrt{2401}=49$
Therefore the value of $\sqrt{2401}$ by prime factorization method is 49.
Note: There is no need to divide the number each time separately. If you divide like shown below then it will save your time which will be very much helpful in competitive exams.
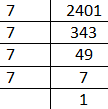
Complete step by step answer:
We will write down the given number first, therefore,
$\sqrt{2401}$
In prime factorization method we have to get the prime factors of the given number and for that we will divide the given number by the lowest number by which it is completely,
As 2401 is completely divisible by the number 7 therefore we get,
$\dfrac{2401}{7}=343$
Therefore 7 is first prime factor of 2401 now we will do the same thing with 343 therefore,
\[\dfrac{343}{7}=49\]
Therefore the second prime factor is also 7, likewise we will proceed and get,
$\dfrac{49}{7}=7$
Therefore,
\[\dfrac{7}{7}=1\]
As the remainder is 1 therefore we can say that we have done with all the prime factors and we have listed below in simplest manner,

Now as we know that the prime factor listed above if multiplies constitutes the given number 2401 therefore we can write,
$\therefore 7\times 7\times 7\times 7=2401$
If we use the formula ${{a}^{m}}{{a}^{n}}={{a}^{m+n}}$ we will get,
$\therefore {{7}^{2}}\times {{7}^{2}}=2401$
As we have to find the square root of the given number therefore taking square roots on the both sides of the equation we will get,
$\therefore \sqrt{{{7}^{2}}\times {{7}^{2}}}=\sqrt{2401}$
If we cancel the square and the square root from the left hand side of the equation we will get,
$\therefore 7\times 7=\sqrt{2401}$
By multiplying and rearranging the above equation we will get,
$\therefore \sqrt{2401}=49$
Therefore the value of $\sqrt{2401}$ by prime factorization method is 49.
Note: There is no need to divide the number each time separately. If you divide like shown below then it will save your time which will be very much helpful in competitive exams.

Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

The number of corners in a cube are A 4 B 6 C 8 D class 8 maths CBSE

Advantages and disadvantages of science

The pH of the gastric juices released during digestion class 8 biology CBSE

What are the methods of reducing friction. Explain




