Question

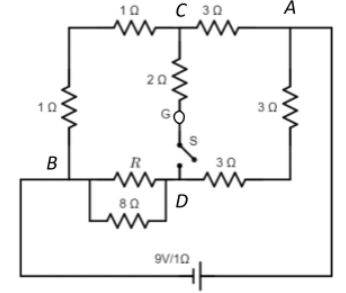
Find the value of R so that no deflection is noticed in the galvanometer when the switch S is closed or open.

A. $4\Omega$
B. $8\Omega$
C. $6\Omega$
D. None of these

Answer 1

Hint: Recognize that the circuit is very similar to that of a Wheatstone bridge. From what is asked of us in the question, we deduce that we are asked for the Wheatstone bridge to be in a balanced condition. Therefore, first calculate the effective resistances across branches AC, CB, AD and DB, and then apply them to the balanced condition of the Wheatstone bridge, which is nothing but equating the ratio of resistance across AC and CB to the ratio of resistances across AD and DB respectively.
Formula Used:
Condition for a balanced Wheatstone bridge: $\dfrac{P}{Q} =\dfrac{R}{S}$, where P and Q are the resistances in one arm of the bridge, and R and S are resistances across the other arm of the bridge.

Complete answer:
Just by looking at the circuit diagram and by understanding that the question asks us to retain no deflection in the galvanometer for a certain value of an unknown resistance we can deduce that the whole setup is basically a Wheatstone bridge.
A Wheatstone bridge, which is also known as a resistance bridge, is a setup that is generally used to calculate an unknown resistance in an arm of the bridge by balancing the two arms of the circuit.
It consists of four effective resistances each connected in one arm of the bridge of which one resistance is unknown. The circuit also consists of a galvanometer and a voltage source.
From the diagram, we see that the galvanometer is connected across CD whereas the voltage source is connected across AB. The current that flows through the galvanometer depends on the potential difference between points C and D.
Therefore, if the ratio of the resistances in the arms of the bridge are equal, then no current flows through the circuit and the galvanometer shows no deflection. This happens when the voltage across opposite branches on each side of the galvanometer becomes equal, and hence there is no potential difference. Under this condition the bridge is said to be balanced.
Now, in the context of the question, we are asked to find the value of R for which there is no deflection in the galvanometer. This means that the resistance R brings about a balance across the circuit.
We now apply the balanced condition of a Wheatstone bridge to our circuit where we get:
$\dfrac{R_{AC}}{R_{CB}} =\dfrac{R_{AD}}{R_{DB}}$
Let us now find the effective resistances across each of the branches.
Branch AB has only one resistance.
$R_{AC} = 3\Omega$
Branch CB has two resistances in series, so effective resistance will be the sum of the two.
$R_{CB} = 1+1 = 2\Omega$
Branch AD also has two resistances in series, so effective resistance will be the sum of the two.
$R_{AD} = 3+3 = 6\Omega$
Branch BD has the unknown resistance and another resistance in parallel. So their effective resistance will be:
$R_{BD} = \dfrac{8R}{8+R}$
Now, we apply the balanced condition with respect to the effective resistances that we found across the arms of the bridge.
$\dfrac{3}{2} =\dfrac{6}{\left(\dfrac{8R}{8+R}\right)}$
$\Rightarrow \dfrac{3}{2} = \dfrac{6(8+R)}{8R}$
$\Rightarrow 3(8R) = 12(8+R) \Rightarrow 24R = 96 +12R \Rightarrow 12R =96 \Rightarrow R =8\Omega$

Therefore, the correct option would be B. $8\Omega$.

Note:
Remember that for this very reason, the Wheatstone bridge is used for the precise measurement of low resistance since the detection of zero current in the galvanometer is also of high precision. It can also be used to measure other quantities like inductance and capacitance. However, for low resistance measurements, a significant error may be introduced due to the resistance of the leads and contacts themselves. Thus, it becomes highly important to have a proper setup.