Question

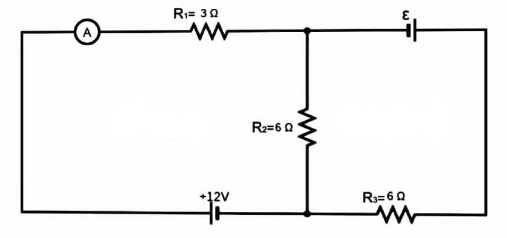
Find the value of emf ($\varepsilon $) when the ammeter reads \[3\,A\] current flowing through it.

A. \[ - 12{\text{ }}volt\]
B. \[6{\text{ }}volt\]
C. \[12{\text{ }}volt\]
D. \[ - 6{\text{ }}volt\]

Answer 1

Hint:In order to solve this question, you must be aware of the concept of Kirchhoff's Voltage Law. It states that for a closed loop series path, the algebraic sum of all the voltages around any closed loop in a circuit is equal to zero. This law is a consequence of charge conservation.

Complete step by step answer:
Kirchhoff's Voltage Law (KVL) asserts that "the total voltage around any closed loop network is equal to the sum of all the voltage drops within the same loop," which is also zero. To put it another way, the algebraic sum of all voltages in the loop must be zero. Kirchhoff's concept is known as the conservation of energy. The current through \[3\Omega \] resistor is \[3A\] .

Hence, Potential difference across it \[ = R \times I = 9{\text{ }}V\].
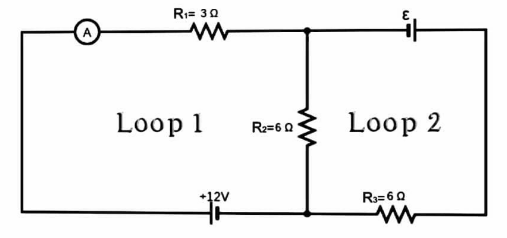
Using Kirchoff’s second law in the closed loop 1,
$12 - 9 - 6i = 0$
$\Rightarrow 3 - 6i = 0$
$\Rightarrow i = \dfrac{1}{2}A$
This means that current through \[3\Omega \] resistor is \[3A\] and current in \[6\Omega \] resistor $\left( {{R_2}} \right)$ is $\dfrac{1}{2}A$ .
Therefore, current flowing in a cell of emf $\varepsilon$ is $\left( {3 - \dfrac{1}{2}} \right)A = \dfrac{5}{2}A$.
Hence, current flowing in 6 ohm resistor $\left( {{R_3}} \right)$ is $\dfrac{5}{2}A$.
Using Kirchoff’s law in closed loop 2,
\[ \Rightarrow - \varepsilon + 6 \times \dfrac{5}{2} - 6 \times \dfrac{1}{2} = 0\]
$ \Rightarrow \varepsilon = 15 - 3$
$\therefore \varepsilon = 12V$

Hence, the correct option is C.

Note:Electromotive force or emf is defined as the electric potential produced but either by electrochemical cell or by changing the magnetic field.A generator or a battery is used for the conversion of energy from one form to another. In these devices, one terminal becomes positively charged while the other becomes negatively charged. Therefore, an electromotive force is a work done on a unit electric charge.