Question

Find the value of $ \cos 30^\circ $ geometrically.

Answer 1

Hint: Here we will first draw an equilateral triangle and perpendicular on the base of the triangle by the vertex. Then find the unknown perpendicular side by using Pythagoras theorem and use the trigonometric identities and place the values in it and simplify the fractions

Complete step-by-step answer:
Let us consider an equilateral triangle $ \Delta XYZ $ and with the sides $ XY = YZ = ZX = 2a $
Also, all the angles of the equilateral triangle is equal to $ 60^\circ $
 $ \therefore \angle X = \angle Y = \angle Z = 60^\circ $

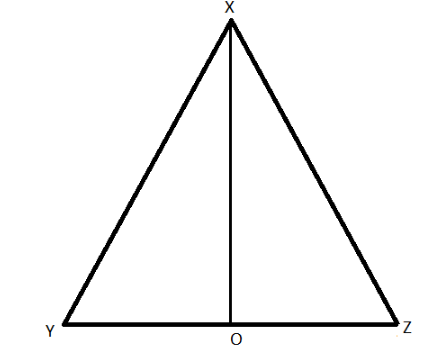
Draw the line of perpendicular from the point “X” on “YZ”
As shown in the above figure,
In $ \Delta XOY $ and $ \Delta XOZ $
 $ XO = XO $ (Common side of the triangles)
Also, $ \angle X0Y = \angle XOZ = 90^\circ $ (Perpendicular angles of the triangles)
 $ XY = XZ $ (Sides of the equilateral triangle are always equal)
Therefore, $ \Delta XYZ \cong \Delta XZO $
By using the concept of the congruent part of the congruent triangle –
 $ YO = OZ $ (C.P.C.T.)
 $ \therefore XO = \dfrac{{2a}}{2} $
Common multiple from the numerator and the denominator cancel each other.
 $ \therefore XO = a $
Now, $ \angle YXO = \dfrac{{60}}{2} $
Common multiple from the denominator and the numerator cancel each other.
 $ \angle YXO = 30^\circ $
Now, using the Pythagoras theorem which states that hypotenuse square is equal to the sum of the square of the opposite side and the square of the adjacent side.
In $ \Delta YOX,\;\angle {\text{O = 90}}^\circ $
 $
  XY = 2a \\
  YO = a \\
  XO = ? \\
  $
 $ X{Y^2} = X{O^2} + Y{O^2} $
Make the required measure the subject –
 $ X{O^2} = X{Y^2} - Y{O^2} $
Take square-root on both the sides of the equation –
 $ \sqrt {X{O^2}} = \sqrt {X{Y^2} - Y{O^2}} $
Square and square-root cancel each other on the left hand side of the equation –
 $ XO = \sqrt {X{Y^2} - Y{O^2}} $
Place the values in the above equation –
 $
  XO = \sqrt {{{(2a)}^2} - {a^2}} \\
  XO = \sqrt {4{a^2} - {a^2}} \\
   \Rightarrow XO = \sqrt {3{a^2}} \\
   \Rightarrow XO = \sqrt 3 a \;
  $
As, cosine function is the ratio of the adjacent side to the hypotenuse.
 $ \cos 30^\circ = \dfrac{{\sqrt 3 a}}{{2a}} $
Common Multiple from the numerator and the denominator cancel each other.
 $ \cos 30^\circ = \dfrac{{\sqrt 3 }}{2} $
So, the correct answer is “ $ \cos 30^\circ = \dfrac{{\sqrt 3 }}{2} $”.

Note: Remember different trigonometric identities and know the difference among them.
Also, follow the different conditions of the congruence of the triangles to prove these types of solutions such as –
I.SSS criteria (Side - Side - Side)
II.SAS criteria (Side – Angle - Side)
III.ASA criteria (Angle – Side – Angle)
IV.AAS criteria (Angle – Angle – Side)
V.RHS criteria (Right angle – Hypotenuse – Side)