Question

Find the value of $ \cos 120{}^\circ $.

Answer 1

Hint: In a right-angled triangle with the length of the side opposite to angle θ as perpendicular (P), base (B) and hypotenuse (H):
 $ \sin \theta =\dfrac{P}{H},\cos \theta =\dfrac{B}{H},\tan \theta =\dfrac{P}{B} $
 $ {{P}^{2}}+{{B}^{2}}={{H}^{2}} $ (Pythagoras' Theorem)
If a point P is at a distance $ r $ from the origin, then the coordinates of the point are $ \left( r\cos \theta,r\sin \theta \right) $, where $ \theta $ is angle made by line OP with the positive direction of the x-axis.
Find the coordinates of a point which is 1 unit far from the origin and makes an angle of $ 120{}^\circ $ with the x-axis. The x-co-ordinate of the point is the value of $ \cos 120{}^\circ $.

Complete step by step answer:
Let us mark a point P on the graph paper, at distance of 1 unit from the origin, such that OP makes an angle of $ 120{}^\circ $ with the positive direction of the x-axis.
From the definition of trigonometric ratios, we know that the x-co-ordinate of the point P is the value of $ \cos 120{}^\circ $ and the y-coordinate is the value of $ \sin 120{}^\circ $.

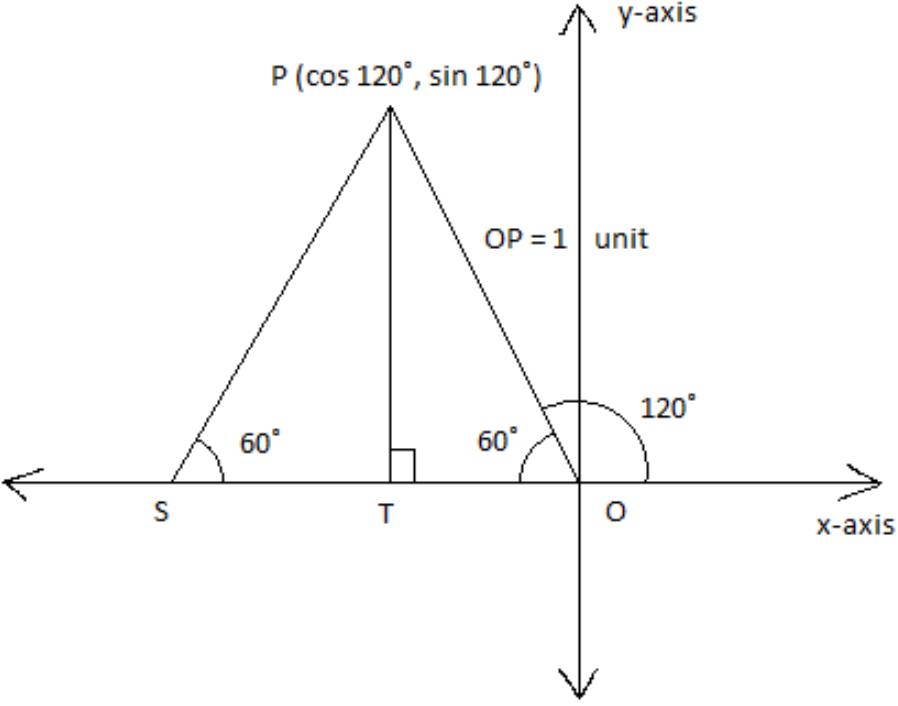
The $ \Delta PSO $ in the above diagram is an equilateral triangle.
∴ $ OP=OS=1 $ ... (1)
Also, $ \Delta PTO\cong \Delta PTS $ ... (Using ASA congruence)
∴ $ ST=OT=\dfrac{1}{2}OS $
⇒ $ OT=\dfrac{1}{2}\times 1=\dfrac{1}{2} $ ... [Using equation (1)]
It means that the coordinates of the point T are $ \left( -\dfrac{1}{2},0 \right) $.
Since the point P is on the perpendicular line at point T, its x-co-ordinate must also be the same as that of T, i.e. $ -\dfrac{1}{2} $.
It follows that $ \cos 120{}^\circ =-\dfrac{1}{2} $.

Note: Now that we know the lengths of OP and OT, we can use Pythagoras' theorem and find PT as well, which is the y-coordinate of P, i.e. $ \sin 120{}^\circ $.
Rule of CAST: In the IV, I, II and III quadrants, $ \cos \theta $, All trigonometric ratios, $ \sin \theta $ and $ \tan \theta $ are positive, respectively.
Trigonometric Ratios for Allied Angles:
 $ \sin \left( -\theta \right)=-\sin \theta $ $ \cos \left( -\theta \right)=\cos \theta $
 $ \sin \left( 2n\pi +\theta \right)=\sin \theta $ $ \cos \left( 2n\pi +\theta \right)=\cos \theta $
 $ \sin \left( n\pi +\theta \right)={{\left( -1 \right)}^{n}}\sin \theta $ $ \cos \left( n\pi +\theta \right)={{\left( -1 \right)}^{n}}\cos \theta $
 $ \sin \left[ (2n+1)\dfrac{\pi }{2}+\theta \right]={{(-1)}^{n}}\cos \theta $ $ \cos \left[ (2n+1)\dfrac{\pi }{2}+\theta \right]={{(-1)}^{n}}\left( -\sin \theta \right) $
If one trigonometric ratio is known, we can use Pythagoras' Theorem and calculate the values of all other trigonometric ratios.