Question

Find the value of $ \arcsin \left( \sin \left( 160{}^\circ \right) \right) $ .
[a] $ 160{}^\circ $
[b] $ 70{}^\circ $
[c] $ -20{}^\circ $
[d] $ 20{}^\circ $

Answer 1

Hint: Use the fact that if $ y=\arcsin x $ , then $ x=\sin y $ . Assume that $ \arcsin \left( \sin \left( 160{}^\circ \right) \right)=y $
Hence form an equation in y. Use the fact that if $ \sin x=\sin y $ then $ x=n\pi +{{\left( -1 \right)}^{n}}y $ . Use the fact that $ \arcsin x\in \left[ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right] $ . Hence find the value of $ \arcsin \left( \sin \left( 160{}^\circ \right) \right) $ .

Complete step-by-step answer:
Complete step-by-step answer:
Before dwelling into the solution of the above question, we must understand how $ {{\sin }^{-1}}x $ is defined even when $ \sin x $ is not one-one.
We know that sinx is a periodic function.
Let us draw the graph of sinx

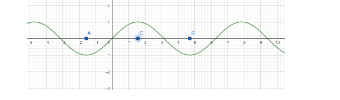
As is evident from the graph sinx is a repeated chunk of the graph of sinx within the interval $ \left[ A,B \right] $ , and it attains all its possible values in the interval $ \left[ A,C \right] $ . Here $ A=\dfrac{-\pi }{2},B=\dfrac{3\pi }{2} $ and $ C=\dfrac{\pi }{2} $
Hence if we consider sinx in the interval [A, C], we will lose no value attained by sinx, and at the same time, sinx will be one-one and onto.
Hence $ \arcsin x $ is defined over the domain $ \left[ -1,1 \right] $ , with codomain $ \left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right] $ as in the domain $ \left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right] $ , sinx is one-one and $ {{R}_{\sin x}}=\left[ -1,1 \right] $ .
Now since $ \arcsin x $ is the inverse of sinx it satisfies the fact that if $ y=\arcsin x $ , then $ \sin y=x $ .
So let $ y=\arcsin \left( \sin \left( 160{}^\circ \right) \right) $
Hence, we have
 $ \sin \left( y \right)=\sin \left( 160{}^\circ \right) $
We know that if $ \sin x=\sin y $ then $ x=n\pi +{{\left( -1 \right)}^{n}}y,n\in \mathbb{Z} $ .
Hence, we have
 $ y=n\pi +{{\left( -1 \right)}^{n}}160\times \dfrac{\pi }{180}=n\pi +{{\left( -1 \right)}^{n}}\dfrac{8}{9}\pi $
Now since $ \arcsin \left( x \right)\in \left[ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right], $ we have $ y\in \left[ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right] $
Taking n =1, we get
 $ y=\pi -\dfrac{8\pi }{9}=\dfrac{\pi }{9} $
Hence $ \arcsin \left( \sin \left( 160{}^\circ \right) \right)=\dfrac{\pi }{9}=\dfrac{180{}^\circ }{9}=20{}^\circ $
Hence option [d] is correct.

Note: [1] The above-specified codomain for arcsinx is called principal branch for arcsinx. We can select any branch as long as $ \sin x $ is one-one and onto and Range $ =\left[ -1,1 \right] $ . Whenever not mentioned, we take the principal branch for the codomain of arcsin(x).
[2] Alternative solution:
We know that $ \arcsin \left( \sin x \right)=\left\{ \begin{matrix}
   \vdots & \vdots \\
   x & ,x\in \left[ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right] \\
   \pi -x & x\in \left[ \dfrac{\pi }{2},\dfrac{3\pi }{2} \right] \\
   \vdots & \vdots \\
\end{matrix} \right. $
Since $ 160{}^\circ \in \left[ \dfrac{\pi }{3},\dfrac{3\pi }{2} \right] $ , we have $ \arcsin \left( \sin \left( 160{}^\circ \right) \right)=180{}^\circ -160{}^\circ =20{}^\circ $
Hence option [a] is correct.
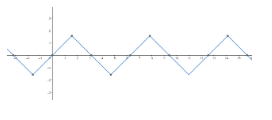
[3] Graph of arcsin(sinx):