Question

Find the thickness of the plate which will produce a change in optical path equal to half the wavelength $\lambda$ of light passing through it normally the refractive index of the plate $\mu$ is-
$A. \dfrac {\lambda}{4(\mu-1)}$
$B. \dfrac {3\lambda}{4(\mu-1)}$
$C. \dfrac {\lambda}{(\mu-1)}$
$D. \dfrac {\lambda}{2(\mu-1)}$

Answer 1

Hint: We have to find the thickness of the plate which will produce change in optical path length equal to $\dfrac {\lambda}{2}$. We know the formula for optical path length in terms of thickness and refractive index. Compare both these equations for change in optical path. Then, rearrange the obtained equation and write the equation for t in terms of all the other parameters. This obtained value is the thickness of the plate which will produce a change in optical path length equal to $\dfrac {\lambda}{2}$.
Formula used:
$\Delta x= (\mu-1)t$

Complete answer:

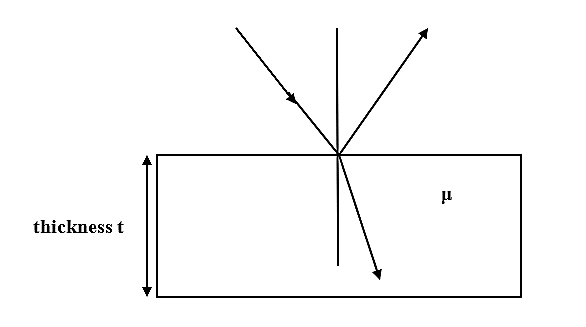
Let t be the thickness of the plate
Given: Change in optical path ($\Delta x$)= $\dfrac {\lambda}{2}$ …(1)
We know,
Optical path difference is given by,
$\Delta x= (\mu-1)t$ …(2)
Where, $\Delta x$ is the optical path difference
            $\mu$ is the refractive index
            t is the thickness of the plate
Comparing equation. (1) and (2) we get,
$\dfrac {\lambda}{2}= (\mu-1)t$
Rearranging the above equation we get,
$t= \dfrac {\lambda}{2(\mu-1)}$
Thus, the thickness of the plate is $\dfrac {\lambda}{2(\mu-1)}$.

So, the correct answer is option D i.e. $\dfrac {\lambda}{2(\mu-1)}$.

Note:
The difference in the path length of two paths is known as Optical path difference, Students should not get confused and know the difference between actual path length and optical path length. Actual path length is the actual difference travelled by the light. Whereas the optical path length is dependent on the refractive index of the material. Optical path length allows us to find out the phase of the light at any point.