Question

Find the surface area of a sphere of diameter: $14cm$

Answer 1

Hint: The relation between diameter of a sphere and radius of a sphere is given as
Diameter of Sphere $ = 2 \times (radius\,\,of\,\,sphere)$
Surface area of sphere $ = 4\pi {r^2}$
where ‘\[r\]’ represents the radius of the sphere.
The value of $\pi $ can be used as $\dfrac{{22}}{7}$ or \[3.14\].

Complete step-by-step answer:

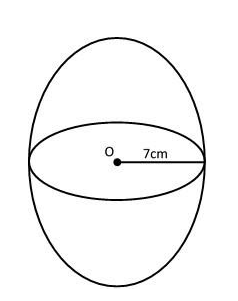
Given that the diameter of the sphere is equal to $14cm$
$\therefore $ Diameter $d = 14\,cm.$
Diameter of sphere $ = 2 \times (radius\,of\,sphere)$
$ \Rightarrow radius\,of\,sphere = \dfrac{{Diameter\,of\,sphere}}{2}$
i.e. $r = \dfrac{d}{2}.$
Now we will find the value of ‘\[r\]’
$r = \dfrac{{14}}{2}$ $ \Rightarrow r = 7\,cm.$
$\therefore $ Surface area of sphere $ = 4\pi {r^2}$
Put the value of ‘\[r\]’ here and use $\pi = \dfrac{{22}}{{7.}}.$
$\therefore $ Surface area of sphere $ = 4 \times \dfrac{{22}}{7} \times 7 \times 7$
$ = 4 \times 22 \times 7$
$ = 88 \times 7$
$ = 616\,c{m^2}\,or\,616\,sq.cm.$

Note: Sphere: In geometry, the set of all the points in three-dimensional space lying at the same distance (the radius) from a given fixed point (the centre), or the result of rotating a circle about one of its diameters. The components and properties of a sphere are analogous to those of a circle. Students must remember to find the value of ‘\[r\]’ radius of the circle as you are given the diameter of the circle'\[d\]’.