Question

How‌ ‌do‌ ‌you‌ ‌find‌ ‌the‌ ‌slope‌ ‌of‌ ‌the‌ ‌line‌ ‌$x=-3$?‌ ‌

Answer 1

Hint: We first try to find the characteristics of the line $x=-3$. We find the relation of the slope of the line with the angle it makes with the positive X-axis. We also find the point at which it intersects the Y-axis.

Complete step-by-step solution:
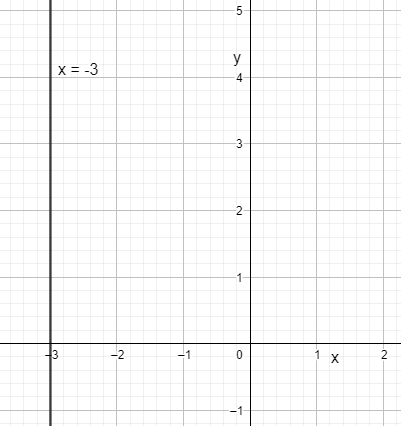
We need to find the slope and y-intercept of the function $x=-3$.
We know that any equation of the form $x=c$ where $c$ is a constant will be a vertical line parallel to the Y-axis. The slope of these equations is always undefined.
Slope is usually defined by the ratio tan of the angle made by a line with the positive X-axis.
In case of vertical lines, they make ${{90}^{\circ }}$ with the X-axis.
We also know $\tan 90$ is undefined. Therefore, the slope of $x=-3$ is undefined.
Now we find the y-intercept of $x=-3$.
As we know that the line is parallel to the Y-axis and we know that parallel lines don’t touch or intersect each other ever. Therefore, there is no y-intercept of the function $x=-3$.

Note: We can also take the equation as a function of $x$ where $f\left( x \right)=x+3$. We know that the slope of any function is the differentiated form of the function equal to $\dfrac{dy}{dx}$. In the Question as function $y$ is not mentioned and we have that $x=-3$, which gives $dx=0$. Division by zero is undefined. Therefore, the slope for $5x-2=0$ is undefined.