Question

Find the shortest and the longest distance from the point (2,-7) to the circle $x^{2}+y^{2}-14x-10y-151=0$.

Answer 1

Hint: In this question it is given that we have to find the shortest and the longest distance from the point (2,-7) to the circle $x^{2}+y^{2}-14x-10y-151=0$. So for finding solution we first draw the diagram,

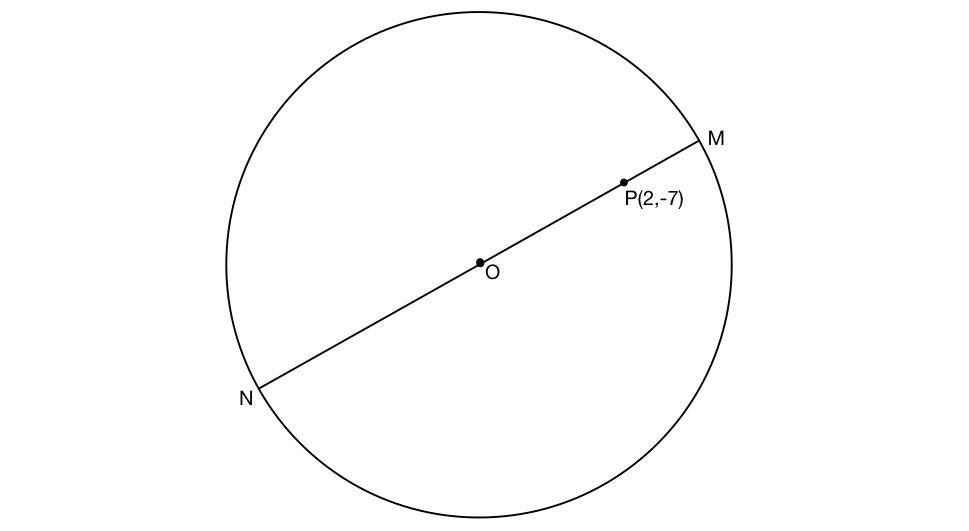
So we have to find the coordinate of the centre O and the radius of the circle i.e, OM=ON=radius. And after that we can easily find the shortest distance PM=OM-OP and longest distance PN=MN-PM.

Complete step-by-step answer:
So before moving into the coordinates first of all we have to determine that the point P(2,-7) lies in which side of circle,
So putting the value x=2, y=-7 in left hand side of the equation we get,
$x^{2}+y^{2}-14x-10y-151$
=$2^{2}+\left( -7\right)^{2} -14\times 2-10\left( -7\right) -151$
=4+49-28+70-151 = -56 <0.
And as we know that if any point (a,b) lies inside the circle then we can write, $a^{2}+b^{2}-14a-10b-151<0$.
So the given point P(2,-7) lies inside the circle.

Now as we know that if any equation of circle is in the form of $x^{2}+y^{2}+2gx+2fy+c=0$ then the centre of the circle is (-g,-f) and the radius is r=$\sqrt{g^{2}+f^{2}-c}$.
So comparing the above equation with the given equation $x^{2}+y^{2}-14x-10y-151=0$, we can easily find that g=-7 and f=-5, so the centre of the circle O(-g,-f)=(7,5) and the radius
 r=OM=ON=$\sqrt{7^{2}+5^{2}-\left( -151\right) }$
  =$\sqrt{49+25+151}$=$\sqrt{225}$=15.

For finding distance we need to know the distance formula i.e, the distance between the points (a,b) to (c,d) is $\mathbf{d} =\sqrt{\left( a-c\right)^{2} +\left( b-d\right)^{2} }$.
So. by the above formula we can find the distance between centre O(7,5) and P(2,-7)
OP=$$\sqrt{\left( 7-2\right)^{2} +\left( 5-\left( -7\right) \right)^{2} }$$
     =$$\sqrt{5^{2}+\left( 12\right)^{2} }$$
     =$$\sqrt{25+144}$$
     =$$\sqrt{169}$$=13.
Then the shortest distance from the point P(2,-7) to the circle,
PM=OM-OP=15-13=2 units.
And the longest distance,
PN=MN-PM=(OM+ON)-PM =(15+15)-2=28 units.

Note: To solve this type of question you need to keep in mind that every point inside the circle must lie on one of its diameters. And then the point divides the diameter into two parts so the length of one part must be the longest one and the other one is the shortest.