Question

How do you find the relative extrema of $f(x)=3{{x}^{5}}-5{{x}^{3}}?$

Answer 1

Hint: For this type of question, we need to calculate the maxima and minima (the relative extrema). For this, we calculate the first derivative and equate that to zero to obtain the critical points. Then we evaluate the second derivative and substitute the obtained solutions in the equation to find out the relative maxima and minima.

Complete step by step solution:
In the given question, we have our equation given $f(x)=3{{x}^{5}}-5{{x}^{3}}$ . We first calculate the first derivative for the given equation.
$\Rightarrow f'(x)=\dfrac{d\left( 3{{x}^{5}}-5{{x}^{3}} \right)}{dx}$
We differentiate each of the terms with respect to x,
$\begin{align}
  & \Rightarrow f'(x)=3.5{{x}^{5-1}}-5.3{{x}^{3-1}} \\
 & \Rightarrow f'(x)=15{{x}^{4}}-15{{x}^{2}} \\
\end{align}$
Taking the term $15{{x}^{2}}$ common out,
$\Rightarrow f'(x)=15{{x}^{2}}\left( {{x}^{2}}-1 \right)......(1)$
The critical points (maxima and minima) are obtained for $f'(x)=0$ .
$\Rightarrow 15{{x}^{2}}\left( {{x}^{2}}-1 \right)=0$
Solving for these equations,
$\begin{align}
  & \Rightarrow 15{{x}^{2}}=0 \\
 & \Rightarrow x=0......(2) \\
\end{align}$
We get 0 as one solution.
$\begin{align}
  & \Rightarrow \left( {{x}^{2}}-1 \right)=0 \\
 & \Rightarrow {{x}^{2}}=1 \\
\end{align}$
Taking square root on both sides,
$x=\pm 1......(3)$
We get the other 2 solutions as +1 and -1. Therefore, the 3 solutions are -1, 0, +1.
We need to evaluate the second derivative now.
$\Rightarrow f''(x)=\dfrac{d\left( 15{{x}^{4}}-15{{x}^{2}} \right)}{dx}$
We differentiate each term with respect to x.
$\begin{align}
  & \Rightarrow f''(x)=15.4{{x}^{4-1}}-15.2{{x}^{2-1}} \\
 & \Rightarrow f''(x)=60{{x}^{3}}-30x \\
\end{align}$
We need to substitute the solutions here, to check if there is a local maxima or minima. If the second derivative is positive, there exists a local minima and if the second derivative is negative, there exists a local maxima.
For $x=0,$
$\Rightarrow f''(x)=60\left( {{0}^{3}} \right)-30\left( 0 \right)=0$
For $x=-1,$
$\Rightarrow f''(x)=60\left( -{{1}^{3}} \right)-30\left( -1 \right)=-60+30=-30$
Since the second derivative is negative, it is a local maxima at $x=-1.$
For $x=1,$
$\Rightarrow f''(x)=60\left( {{1}^{3}} \right)-30\left( 1 \right)=60-30=30$
Since the second derivative is positive, it is a local minima at $x=1.$

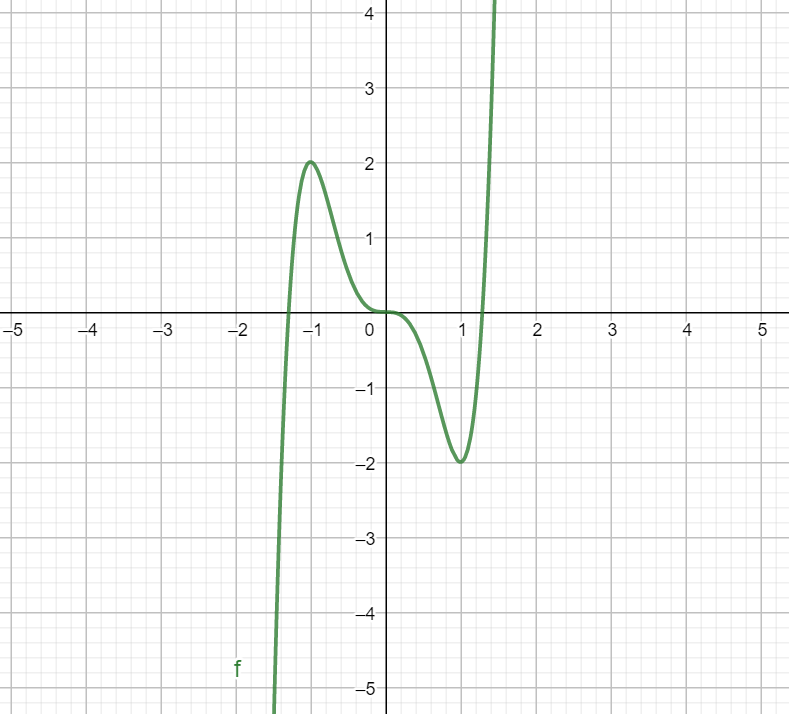
Above is the graph for the function f(x). As we can see, it has a local maxima at $x=-1$ and a local minima at $x=1.$

Note: While solving this question, the students need to be careful while differentiating and simplifying since it is the differentiation of higher order terms. We also can solve this problem solely graphically by just plotting the function and noticing the local maxima or minima through the graph.